Question 157686: Hi, can you please help, can you please help with this piecewise defined function
.
Piecewise defined function
.
f(x) = { x - 4,  } }
.........{ 2x + 3,  } }
.........{ 36,  } }
.
I think the domain is ( 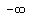 , , ) )
.
I think the range is ( 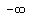 , ,  ] U ( ] U (  , ,  ] U { ] U {  } }
.
Is this domain, and range right? Can you please confirm? Please use interval notation, just like what I used for the domain and range
.
Thanks ahead of time, Levi
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) = { x - 4,  } }
.........{ 2x + 3,  } }
.........{ 36,  } }
f is defined using three formulas for linear function, so graph all three of them
graph first this linear function:  , for , for  ...........since we have a restriction ...........since we have a restriction  , erase the part , erase the part 
the domain is (  , , ) )
then graph this linear function:  , for , for  ...........since we have a restriction ...........since we have a restriction  , erase the part from , erase the part from  to to  and the part where and the part where 
this graph will be a line segment from  to to 
the domain is (  , ,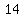 ) )
then graph this linear function:  , for , for 
this is constant function, so it is define for [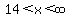 ) )
the domain is [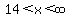 ) )
|
|
|