Question 157193: I dont understand what im supposed to do for this problem:
without graphing, determine if the graphs of each pair of equations are parallel, perpendicular or neither.
2y=8x+4 and y=-1/4x
Answer by Earlsdon(6294)   (Show Source):
You can put this solution on YOUR website! You can do this without graphing by finding the slope of each equation.
Remember the "slope-intercept" form? y = mx+b where m is the slope.
Starting with the given equations, get them into the slope-intercept form so that you campare their slopes:
First equation:
 To get y by itself, you divide both sides by 2.
 and you can see that the slope,  .
Second equation:
 as you can see, this is already in the slope-intercept form and the slope here is: 
Ok, we have the two slopes...now what?
Well, we compare them!
Why, because we know (or should know) that if two lines are parallel, their slopes are equal, and if two lines are perpendicular, their slopes are negative reciprocals.
So what is the negative reciprocal of  ? Why, it's just  .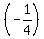
So you can see that the slopes are negative reciprocals, therefore, the two lines are perpendicular!...and all this without graphing.
|
|
|
