|
Question 156745: 2x-2y=15
4x+4y=10
Help, I need to solve for x and y
Found 2 solutions by Earlsdon, Electrified_Levi:
Answer by Earlsdon(6294)   (Show Source):
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
2x-2y=15
4x+4y=10
Help, I need to solve for x and y
.
First, you can reduce the second equation, by multiplying each side by "2"
.
 =  = =  = 
.
The second equation  is reduced to 
.
The Two equations are
.
.
.
This is the way I usually solve these equations, First, solve for a letter(usually the easiest letter), we will solve for "x" in both equations
.
Equation 1 =
.
Now we will move (-2y) to the right side
.
=  = 
.
We will rearrange the numbers
.
= 
.
We will divide each side by "2" to get "x"
.
 = 
.
Our first "x" =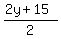 
.
Now let's solve "x" in our second equation,
.
We will move (2y) to the right side
.
=  = 
.
We will rearrange the numbers
.
= 
.
We will divide each side by "2" to get "x"
.
=  = 
.
Our second "x" = 
.
Since "x" is one number, and "x" equals our two answers, our answers equal each other, we can put our two answers in an equation
.
Answer 1 =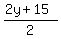
.
Answer 2 =
.
.
We will now solve for "y"
.
.
We will use cross multiplication
.
 = 
.
It will become 
.
We will rearrange numbers
.
= 
.
We will use the distribution method
.
 =
.
 =
.
.
Now we will solve for "y", we will move (-4y) to the left
.
=  = 
.
Now we will move (30) to the right side
.
=  = 
.
Now to find "y" we will divide each side by "8"
.
=  =  , if we reduce 
.
y =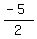 
.
To find "x" all you do is substitute "y" with 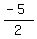in one of our original equations
.
.
.
Let's use the second equation(replace "y" with )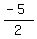
.
=  =  = 
.
We will move (-5) over to the right side
.
=  = 
.
Now we will divide each side by "2" to get "x"
.
 =  = 
.
x =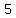 
.
We can check our answers by replacing "x" and "y" with our answers we got, in our very first equations
.
x =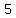
.
y =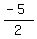
.
Let's replace "x" and "y" with the numbers above
.
=  =  =  =  (True)
.
=  =  =  =  (True)
.
This method will work for all problems like this
.
x =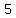
.
y =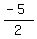
.
The ordered pair is (x,y), our ordered pair is (5, )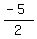
.
Hope I helped, Levi
|
|
|
| |
