Question 156683: For the exponential function e^x and logarithmic function log x, graphically show the effect if x is doubled.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Jump to transformations of the logarithmic function
# 1
First let's calculate the values for 
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 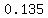
So if  , then , then  . So we have the point (-2,0.135) . So we have the point (-2,0.135)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 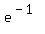 to get to get 
So if  , then , then  . So we have the point (-1,0.368) . So we have the point (-1,0.368)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 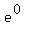 to get to get 
So if  , then , then  . So we have the point (0,1) . So we have the point (0,1)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 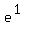 to get to get 
So if  , then , then  . So we have the point (1,2.718) . So we have the point (1,2.718)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 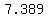
So if  , then , then  . So we have the point (2,7.389) . So we have the point (2,7.389)
Now let's plot these points

Now draw a line through the points to graph 

================================================
# 2
Now let's calculate the values for 
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 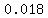
So if  , then , then  . So we have the point (-2,0.018) . So we have the point (-2,0.018)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 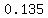
So if  , then , then  . So we have the point (-1,0.135) . So we have the point (-1,0.135)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate 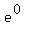 to get to get 
So if  , then , then  . So we have the point (0,1) . So we have the point (0,1)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 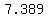
So if  , then , then  . So we have the point (1,7.389) . So we have the point (1,7.389)
--------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate 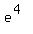 to get to get 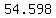
So if  , then , then  . So we have the point (2,54.598) . So we have the point (2,54.598)
Now let's plot these points

Now draw a line through the points to graph 

Notice how the graph of  is much steeper than the graph of is much steeper than the graph of  . This is because the values of . This is because the values of  are simply the values of are simply the values of  squared (since squared (since  ). For instance, if ). For instance, if  , then , then  and and  . Since . Since  is the square of is the square of  , this verifies our claim. So the transformation that occurs on , this verifies our claim. So the transformation that occurs on  is a horizontal compression (since we are dealing with "x" and the graph gets thinner). is a horizontal compression (since we are dealing with "x" and the graph gets thinner).
======================================================
Jump to transformations of the exponential function
# 3
Now let's calculate the values for 
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 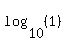 to get to get 
So if  , then , then  . So we have the point (1,0) . So we have the point (1,0)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 
So if  , then , then  . So we have the point (2,0.301) . So we have the point (2,0.301)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 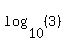 to get to get 
So if  , then , then  . So we have the point (3,0.477) . So we have the point (3,0.477)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 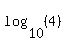 to get to get 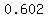
So if  , then , then  . So we have the point (4,0.602) . So we have the point (4,0.602)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Use a calculator to evaluate Use a calculator to evaluate 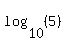 to get to get 
So if  , then , then  . So we have the point (5,0.699) . So we have the point (5,0.699)
Now let's plot the points

Now connect the points to graph 

=============================================================================
# 4
Now let's calculate the values for 
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 
So if  , then , then  . So we have the point (1,0.301) . So we have the point (1,0.301)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate 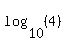 to get to get 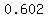
So if  , then , then  . So we have the point (2,0.602) . So we have the point (2,0.602)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate  to get to get 
So if  , then , then  . So we have the point (3,0.778) . So we have the point (3,0.778)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate 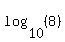 to get to get 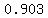
So if  , then , then  . So we have the point (4,0.903) . So we have the point (4,0.903)
----------------------------------------
Let's find the y value when 
 Start with the given equation Start with the given equation
 Plug in Plug in 
 Multiply Multiply  and and  to get to get 
 Use a calculator to evaluate Use a calculator to evaluate 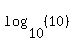 to get to get 
So if  , then , then  . So we have the point (5,1) . So we have the point (5,1)
Now let's plot the points

Now draw a curve through the points to graph 

By comparing  and and  , we can see that the graph of , we can see that the graph of  is simply the graph of is simply the graph of  shifted up some number of units. So a vertical translation has occured on shifted up some number of units. So a vertical translation has occured on  to get to get 
|
|
|