|
Question 156591: 1.x^4=5x^2
2.x^4+18x^3+8x+144=0
3.x^3+19x^2-7x-133=0
4.x^6-13x^5-7x=-91
I need help solving these. So far I have spent hours on just these problems our teacher doesn't explain things very well.
Thanks
Lauren
Found 2 solutions by stanbon, Earlsdon:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.x^4=5x^2
x^4 - 5x^2 =
x^2 (x^2 - 5) = 0
x^2 (x-sqrt(5))(x+sqrt(5)) = 0
x = 0 or x = sqrt(5) or x = -sqrt(5)
---------------------------------
2.x^4+18x^3+8x+144=0
x^3(x+18) + 8(x+18) = 0
(x+18)(x^3+8) = 0
(x+18)(x+2)(x^2-2x+4) = 0
x = -18 or x = -2 or x^2-2x+4 =0
---
Use the quadratic formula on x^2-2x+4
x = [2 +- sqrt(4 - 4*1*4)]/2
x = [2 +- sqrt(-12)]/2
x = [1 +- isqrt(3)]
----------------------------------
3.x^3+19x^2-7x-133=0
x^2(x + 19) -7(x+19) = 0
(x+19)(x^2-7) = 0
(x+19)(x-sqrt(7))(x+sqrt(7)) = 0
x = -19 or x=sqrt(7) or x=-sqrt(7)
----------------------------------
4.x^6-13x^5-7x=-91
x^6 - 13x^5 -7x + 91 = 0
x^5(x-13) - 7(x-13) = 0
(x-13)(x^5-7) = 0
x = 13 and x = 7^(1/5)
=============================
Cheers,
Stan H.
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve for x:
1)  Divide both sides by Divide both sides by 
 Factor out an Factor out an 
 Apply the zero product rule: If a*b = 0, then either a = 0 or b = 0 or both. Apply the zero product rule: If a*b = 0, then either a = 0 or b = 0 or both.
 or or 
If  then then  and and 
If  then then  Take the square root of both sides to get: Take the square root of both sides to get:
 or or 
Now because this is a fourth degree polynomial, you can expect four solutions, some of which may be identical.
The solutions are:




--------------------------------
2)  This polynomial can be factored into: This polynomial can be factored into:
 and the first factor can be further factored as it is the sum of two cubes and the first factor can be further factored as it is the sum of two cubes 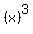 and and  , so we get: , so we get:
 Now, applying the zero product rule that was used in the first problem, you will set each of these three factors equal to zero. Now, applying the zero product rule that was used in the first problem, you will set each of these three factors equal to zero.
 Here, Here, 
 Here, we'll have to use the quadratic formula to solve for x: Here, we'll have to use the quadratic formula to solve for x:  and a = 1, b = -2, and c = 4, so... and a = 1, b = -2, and c = 4, so...
 Simplifying this, we get: Simplifying this, we get:



 or or  Simplifying this: Simplifying this:
 or or 
...and for the last one:


So, as in the first problem, because you have a fourth degree polynomial, you can expect four solutions, and they are:




-----------------
3)  You can solve this by "factoring by grouping" You can solve this by "factoring by grouping"
 Now factor each of the two terms: Now factor each of the two terms:
 Factor out the common factor of Factor out the common factor of 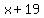
 Apply the zero product rule. Apply the zero product rule.
 or or  so... so...
 or or 
 Take the square root of both sides. Take the square root of both sides.
 or or 
The three solutions are:



----------------
I'll get you started on the last one but see if you can finish it up yourself.
4)  Add 91 to both sides. Add 91 to both sides.
 Factor by grouping. Factor by grouping.
 Factor an Factor an 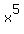 from the first term and a 7 from the second term. from the first term and a 7 from the second term.
 Now factor the common factor Now factor the common factor 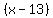
 Apply the zero product rule. Apply the zero product rule.
 or or 
Can you finish this?
|
|
|
| |