Question 156434This question is from textbook
: The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 times the other. Find the numbers
This question is from textbook
Found 2 solutions by nerdybill, Electrified_Levi:
Answer by nerdybill(7384)   (Show Source):
You can put this solution on YOUR website! The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 times the other. Find the numbers
.
Let x = one of the numbers
and y = the other number
.
Because we have two unknowns, we'll need to find two equations.
.
From:"The sum of two numbers is 15." we get equation 1:
x + y = 15
.
From:"Three times one of the numbers is 11 less than 5 times the other." we get equation 2:
3x = 5y - 11
.
Solve equation 1 for y:
x + y = 15
y = 15 - x
.
Substitute the above into equation 2 and solve for x:
3x = 5y - 11
3x = 5(15 - x) - 11
3x = 75 - 5x - 11
3x = 64 - 5x
8x = 64
x = 8
.
Substitute the above into equation 1 and solve for y:
x + y = 15
8 + y = 15
y = 15-8
y = 7
.
Solution: the two numbers are 7 and 8
Answer by Electrified_Levi(103)  (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
The sum of two numbers is 15. Three times one of the numbers is 11 less than 5 times the other. Find the numbers
.
First, we have to find the two equations, we have two unknowns, we will use "x" and "y", "y" will be the larger number
.
First equation, you just add the "x" and "y" to get 15, ( equation =  )
.
Second equation, "Three times one of the numbers" ( It takes 3 times a number to make 11 less than 5 times another)(It takes more of the smaller number to make the larger number) means that the first side of the equation is the bigger number, we can rewrite the equation as " Three times the larger number is 11 less than 5 times the smaller number". ( equation =  )
.
Our two equations are
.
.
.
The way I solve these equations is,
.
First, solve for a letter in both equations(doesn't matter which one, we will solve for "y", since it is already partially solved)(I solve for the easiest letter/ least work to solve)
.
First equation, , we need to move "x" to the other side
.
=  = 
.
We will rearrange the answer, = 
.
Our answer for our first equation is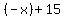 
.
Now solve "y" in our second equation, ,
.
All we have to do to solve for "y" is divide each side by "3"
.
=  = 
.
Our answer for Equation 2 is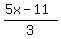 
.
 since both of our answers equal "y", we can put them together in an equation, our answers equal each other
.
.
Now we just solve for "x"
.
= 
.
We use cross multiplication
.
=  = 
.
 rearranging we get 
.
We use distribution method,
.
=  = 
.
It becomes  ,(remember to use the addition, and subtraction signs while multiplying) we will now solve for "x" by bringing (-3x) to the right side
.
=  = 
.
We will move (-11) to the left side
.
=  = 
.
.
Now to find "x" divide each side by "8"
.
=  
.
 "x" = 7,
.
We can replace "x" with "7" in one of our equations, we will use the first one
.
=  , subtract "7" from both sides,  , we get
.
.
"x" = "7"
"y" = "8"
.
We can check by replacing "x" and "y" in both of our equations
.
=  =  (True)
.
=  =  =  ( True )
.
"x" = 7
"y" = 8
.
Three times "8"(y) is 11 less than 5 times "7"(x) (True)
.
Hope I helped, Levi
|
|
|
