show that the equations  and
and  have no real common solution for all values of k.
have no real common solution for all values of k.
 Set the right side of the first equation equal to
the right side of the second equation, since both
equal to y:
Set the right side of the first equation equal to
the right side of the second equation, since both
equal to y:
 Distribute to remove the parentheses:
Distribute to remove the parentheses:
 Get 0 on the left side by adding
Get 0 on the left side by adding 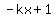 to both sides:
to both sides:

 Swap sides:
Swap sides:
 Group the last two terms on the left in
parentheses:
We need to find the DISCRIMINANT
Group the last two terms on the left in
parentheses:
We need to find the DISCRIMINANT

 is the same as
is the same as
 So
So  ,
,  ,
, 




 There are no real solutions when the
There are no real solutions when the
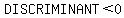 and
and 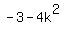 is ALWAYS negative,
since
is ALWAYS negative,
since  is never negative.
So there can be no real common solutions
for any real value of
is never negative.
So there can be no real common solutions
for any real value of  .
Edwin
.
Edwin