Question 156349: A stamp collection consist of 3, 8 and 15 cent stamps. The number of 8 cent stamps is one less than triple the number of 3 cent stamps. The number of 15 cent stamps is six less than the number of 8 cent stamps. The total value of all the stamps is $2.47. Find the number of 8 cent stamps in the collection.
Found 3 solutions by oscargut, kdr, Electrified_Levi:
Answer by oscargut(2103)   (Show Source): (Show Source):
Answer by kdr(11)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let t = number of three cent stamps, e = number of eight cent stamps, and f = number of fifteen cent stamps.
Since the number of 8 cent stamps is one less than triple the number of 3 cent stamps, we can write this equation:
e = 3t - 1
Since the number of 15 cent stamps is six less than the number of 8 cent stamps, we can write this equaation:
f = e - 6
Let's substitute 3t-1 for e:
f = 3t-1-6
f =3t-7
We can write an equation showing the total value of the stamps like this:
.03t + .08e + .15f = 2.47
Now, since we have e and f in terms of t, let's substitute those expressions in the total equation:
.03t + .08(3t-1) + .15(3t-7) = 2.47
Expanding we get:
.03t + .24t - .08 + .45t - 1.05 = 2.47
Combining like terms we now have:
(.03 + .24 + .45)t - 1.13 = 2.47
.72t - 1.13 = 2.47
Adding 1.13 to both sides, we now have:
.72t = 3.60
Dividing both sides by .72, we get:
.72t/.72 = 3.6/.72
t = 5
Putting t into the first equation we had, we get:
e = 3(5) - 1, so e = 14
and putting 14 for e in the second equations, we get:
f = 14 - 6, so f = 8
Finally, we have 5 three cent stamps, 14 eight cent stamps, and 8 fifteen cent stamps.
Checking the result:
5(.03) + 14(.08) + 8(.15) = 2.47
.15 + 1.12 + 1.20 = 2.47
2.47 = 2.47
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
First we have to assign variables for each stamp,(since the 8 cent, and 15 cent stamps rely on the 3 cent stamps [ The number of 8 cent stamps is one less than triple the number of "3 cent" stamps.] The number of the 15 cent stamps rely on the 8 cent stamps, which in turn rely on the 3 cent stamps
.
We can name the number of 3 cent stamps, "x"
.
The number of 8 cent stamps is one less than triple the number of 3 cent stamps = "3x - 1"
.
The number of 15 cent stamps is six less than the number of 8 cent stamps. = "(3x-1) - 6 ", " 3x - 1 - 6 ", or " 3x - 7 "
.
Number of 3 cent stamps = "x"
Number of 8 cent stamps = " 3x - 1 "
Number of 15 cent stamps = " 3x - 7 "
.
Since all the numbers of stamps add up to a value of $2.47, or 247 cents ( we will change the dollars to cents, so we don't have to use a decimal point in our equation)
.
Since it has told us the total value of the stamps, we have to add the stamp value multiplied by the number of stamps( example 3(value)(x)(number of stamps) =  ) )
.
we need to add the stamp value multiplied by the number of stamps, add all three stamps(3 cent stamps, 8 cent stamps, 15 cent stamps) together, which add up to 247 cents, here is the equation
.

.
Now all we need to do is solve for "x", first, we get rid of the parentheses, and use the distribution method
.
 = = 
.
We will rearrange the numbers = 
.
We will combine like terms
.
 = [(3x + 24x + 45x)(- 8 - 105) = 247] = = [(3x + 24x + 45x)(- 8 - 105) = 247] = 
.
Now we need to move (-113) to the right side
.
 = =  = = 
.
We can now divide each side by "72" to find "x"(number of 3 cent stamps)
.
 = =  = =  = = 
.
"x" = 5, here are the numbers of each stamp, in variable form, we can now find how many of each kind of stamp the collection had, ( We found that "x" is 5, just replace "x" with "5" in each equation
.
Number of 3 cent stamps = "x" = "5"
Number of 8 cent stamps = " 3x - 1 " = 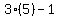 = = 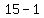 = "14" = "14"
Number of 15 cent stamps = " 3x - 7 " = 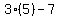 = = 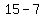 = "8" = "8"
.
We can check our answers by replacing "x" with "5" in our equation
.
 = = 
.
 = = 
.
 = = 
.
 = = 
.
 = =  (True) (True)
.
Number of 3 cent stamps = "5"
Number of 8 cent stamps = "14" ( The number of 8 cent stamps is one less than triple the number of 3 cent stamps = 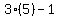 = =  ) (True) ) (True)
Number of 15 cent stamps = "8" ( The number of 15 cent stamps is six less than the number of 8 cent stamps =  ) (True) ) (True)
.
Here are the three answers
.
Number of 3 cent stamps = "5"
Number of 8 cent stamps = "14"
Number of 15 cent stamps = "8"
.
Hope I helped, Levi
|
|
|