SOLUTION: y=x-1 [over] x+4. Find the x and y intercepts along with the asymptotes. Sketch tehe graph. Please help me, I really have no idea what to do with rational functions!!!

First find the equation of vertical asymptote(s), if any, 
by setting the denominator equal to zero:




So  is the equation of the vertical asymptote.

Let's draw that vertical asymptote:



Now let's find the horizontal asymptotes by whichever of
these rules applies:

Rules for horizontal asymptotes:

1. If the largest exponent of x in the numerator is GREATER than the
largest exponent of x in the denominator, there is 
.

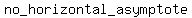2. If the largest exponent of x in the numerator is LESS than the
largest exponent of x in the denominator, the horizontal asymptote is the
x-axis, whose equation is 



3. If the largest exponent of x in the numerator is EQUAL to the
largest exponent of x in the denominator, the horizontal asymptote is 
horizontal line whose equation is

  

---------------------

 or

. 


The largest exponent of x in the numerator is 1, and the
largest exponent in the denominator is also 1, so they are
equal.  So we use rule 3.  The coefficients are both 1.



so the equation of the horizontal asymptote is

 or



So we draw the horizontal asymptote on the same set of axes:

 

Next we get a point on each side of the vertical
asymptote:

Choose x=-5 to get a point on the left side of the
vertical asymptote:




  

So a point on the left side of the vertical asymptote
is (-5,6)

Let's plot that point:



Now we'll sketch in a curve on the left side of that 
vertical asymptote that goes through that point and 
that also gets closer and closer to both the vertical 
and the horizontal asymptote, like this:



Choose x=-3 to get a point on the right side of the
vertical asymptote:




  

So a point on the right side of the vertical asymptote
is (-3,-4)

Let's plot that point too:



Now we'll sketch in a curve on the right of the vertical
asymptote that goes through that point and  that also gets 
closer and closer to both the vertical and the horizontal 
asymptote, like this:



That's it!  It has two parts, one on each side of the
vertical asymptotes.  

Oh, I almost forgot.  You wanted the x and y intercepts, too.
We didn't need them at all for the graph, but we'll get them.

To get the x-intercept, let



Multiply both sides by 



So the x-intercept is (1,0).
That's where the curve crosses the x-axis,

To get the y-intercept, let






So the y-intercept is (0,).
That's where the curve crosses the y-axis,
just a tad below the origin. In this case,
they don't help us much with the graph,
but in some problems they do.

------------
 
(In some problems, you have two or more
vertical asymptotes, so in those, you get 
points in between them as well as on each
side of them).

Edwin