I am completely lost on how to solve augmented matrices.
If you could show me step by step how to solve the
following equation it would be great.
3x + 4y = 11
x + 3y = 2
I know you have to break it down like this
[ 3 4 11]
[ 1 3 2]
After this however I am lost.
You have to end up with a matrix that
looks like this:
[ 1 0 #]
[ 0 1 #]
Then the solutions for x and y will appear
where the #'s are.
We get the 0's first, then we get the 1's:
Your augmented matrix is:
[ 3 4 11]
[ 1 3 2]
Get a 0 where the 1 is:
Multiply the bottom row through by -3
[ 3 4 11]
[-3 -9 -6]
Add the top row to the bottom row but
leave the top row as it is:
[ 3 4 11]
[ 0 -5 5]
Get a 0 where the 4 is:
Multiply the top row by 5 and the bottom
row by 4:
[15 20 55]
[ 0 -20 20]
Add the bottom row to the top row but keep
the bottom row as it is.
[15 0 75]
[ 0 -20 20]
Get a 1 where the 15 is by dividing the
top row through by 15
Get a 1 where the -20 is by dividing the
bottom row through by -20
[ 1 0 5]
[ 0 1 -1]
The two numbers in the right-most colum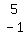n 
are the answers:
x = 5, and y = -1
Edwin
