Question 155544: On the worksheet it shows the equation:
 The first thing i tried to do was get rid of the fraction by mutiplying by the LCD, which i figured would be (z)(2z)(5z)(z+1). however it ended up being a jumbled mess and left me very confused and now I have no idea what to do.
Found 2 solutions by scott8148, Edwin McCravy:
Answer by scott8148(6628)   (Show Source):
You can put this solution on YOUR website! you're using the right technique, but your LCD has too many z's - one is enough
LCD is (z) times (2), (already have the z), times (5), times (z+1)
(10(z+1))-(5(z+1))-(2(z+1))=10(10z) __ 10z+10-5z-5-2z-2=100z __ 3z+3=100z __ 3=97z __ 3/97=z
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website! Edwin's solution:
On the worksheet it shows the equation:
The first thing i tried to do was get rid of the fraction by mutiplying by the LCD, which i figured would be (z)(2z)(5z)(z+1). however it ended up being a jumbled mess and left me very confused and now I have no idea what to do.
You are a little confused on how to find the LCD.
You don't need to repeat the factor z in the LCD.
You only need it ONCE in the LCD, not three times!!!
Let's put parentheses around every term:
The factors of the denominators are z, 2, 5, and z+1
The factor z appears 1 time in the first fraction, 1 time in the second
fraction, 1 time in the third fraction and 0 times in the fourth fraction.
The most number of times that z appears in any ONE denominator is
1 time. Therefore z needs to appear only 1 time in the LCD.
---
The factor 2 appears 0 times in the first fraction, 1 time in the second
fraction, 0 times in the third fraction and 0 times in the fourth fraction.
The most number of times that 2 appears in any ONE denominator is
1 time. Therefore 2 needs to appear only 1 time in the LCD.
---
The factor 5 appears 0 times in the first fraction, 0 times in the second
fraction, 1 time in the third fraction and 0 times in the fourth fraction.
The most number of times that 5 appears in any ONE denominator is
1 time. Therefore 5 needs to appear only 1 time in the LCD.
---
The factor z+1 appears 0 times in the first fraction, 0 times in the second
fraction, 0 times in the third fraction and 1 time in the fourth fraction.
The most number of times that z+1 appears in any ONE denominator is
1 time. Therefore z+1 needs to appear only 1 time in the LCD.
---
Therefore, the LCD is (z)(2)(5)(z+1) or 10z(z+1). We put the LCD
over 1 like this 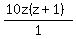 and multiply it by every term:
Now we cancel away the denominators:
 
That's an ugly solution, but it's correct!
Edwin
|
|
|
