
 иии
иии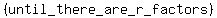 So,
So,  and
and  Substituting,
Substituting,
 Get a 0 on the right:
Get a 0 on the right:
 factor out
factor out 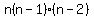
 Simplify the last parentheses:
Simplify the last parentheses:


 Factor the last parentheses:
Factor the last parentheses:
 Setting each factor = 0, we get the
solutions:
Setting each factor = 0, we get the
solutions:
 ,
,  ,
,  ,
,  ,
,  .
The first three are considered correct,
because when
.
The first three are considered correct,
because when 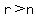 ,
,  And
And  is a solution. But the last one
is a solution. But the last one
 is not a solution because permutations
are not defined for negative numbers.
So the four solutions are
is not a solution because permutations
are not defined for negative numbers.
So the four solutions are
 ,
,  ,
,  ,
,  Possibly your teacher may want only
the solution
Possibly your teacher may want only
the solution  ; however, the first
three are solutions since they cause
both sides of the original equation
to equal 0.
Edwin
; however, the first
three are solutions since they cause
both sides of the original equation
to equal 0.
Edwin