Factor
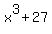Let's write it this way
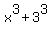That is the sum of two cubes.
Now what if we dropped those cubes and had 
Then suppose we divided that into 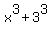by
long division:
x² - 3x + 9
-------------------
x + 3)x³ + 0x² + 0x + 27
x² + 3x²
--------
-3x² + 0x
-3x² - 9x
---------
9x + 27
9x + 27
-------
0
That gives a zero remainder. So you now
know from that, that
x³ + 27
or
x³ + 3³
factors as
(x + 3)(x² - 3x + 9)
But if you learn the principle then you
wouldn't have to use long division. Sure, if
you forgot the principle you could use
long division every time. But you should
memorize the principle to save time.
The principle is
When you have the sum of two cubes
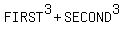it factors as
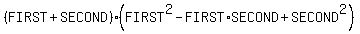So in the case of
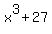You write it as
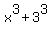Then 
and 
so
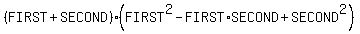becomes
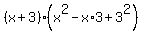or
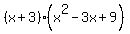Then you don't have to use long division.
-----------------------------------------------
Suppose, instead it were
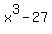Let's write it this way
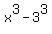That is the DIFFERENCE of two cubes.
Now what if we dropped those cubes and had 
Then suppose we divided that into 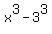by
long division:
x² + 3x + 9
-------------------
x - 3)x³ + 0x² + 0x + 27
x² - 3x²
--------
3x² + 0x
3x² - 9x
---------
9x + 27
9x + 27
-------
0
That gives a zero remainder. So you now
know from that, that
x³ - 27
or
x³ - 3³
factors as
(x - 3)(x² + 3x + 9)
But if you learn the principle then you
wouldn't have to use long division. Sure, if
you forgot the principle you could use
long division every time. But you should
memorize the principle to save time.
The principle is
When you have the sum of two cubes
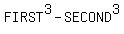it factors as
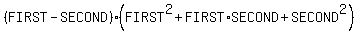So in the case of
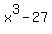You write it as
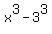Then and
so
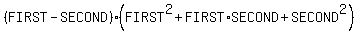becomes
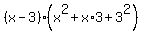or
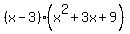Then you don't have to use long division.
---------
In general
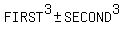factors as
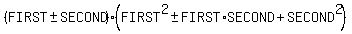Edwin
