|
Question 154259: Help evaluate the determinate? Please explain everything so I can comprehend this...please.
|1 -3 2 0|
|-3 -1 0 -2|
|2 1 3 1|
|2 0 -2 0
Found 2 solutions by Edwin McCravy, Alan3354:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Help evaluate the determinate? Please explain everything so I can comprehend this...please
| 1 -3 2 0|
|-3 -1 0 -2|
| 2 1 3 1|
| 2 0 -2 0|
Pick a row of column, with the most 0's in it
that you can find, and use row and/or column
operations to get all but one 0 in that row
or column.
The red row below already has two 0's,
| 1 -3 2 0|
|-3 -1 0 -2|
| 2 1 3 1|
| 2 0 -2 0|
and all we have to do to get a 0 where that
red -2 is on the bottom row, is to add the
numbers in the first column to the corresponding
numbers in the third column. We get this:
| 1 -3 2+1 0|
|-3 -1 0-3 -2|
| 2 1 3+2 1|
| 2 0 -2+2 0|
or
| 1 -3 3 0|
|-3 -1 -3 -2|
| 2 1 5 1|
| 2 0 0 0|
Now all the numbers on the bottom row are 0's
all except for one, the 2 in the lower left
corner.
So let's cross out all the other elements in the
same row and column that that 2 is in:
| 1 -3 3 0|
|-3 -1 -3 -2|
| 2 1 5 1|
| 2 0 0 0|
Now multiply that 2 by the 3x3 determinant formed
by the 9 numbers in the upper right:
|-3 3 0|
( )2×|-1 -3 -2|
| 1 5 1|
But we must now check the sign scheme to see whether
we keep the positive sign of the 2 or whether we must
change its sign to get its opposite, -2.
This is the sign scheme for the 4x4 determinant.
 Notice that since the 2 is in the bottom left hand
corner and there is a - in the bottom left-corner in
the sign scheme, we must change the sign of the 2, to
a -2. (If the 2 had been in a position where there is a
+ sign in the sign scheme, we would have have just kept
the sign and used 2.)
So we have:
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
Now we have to expand that determinant. So we
pick a row with the most 0's in it, and use row
and/or column operations to get all but one 0
in that row or column.
The top (red) row below already has one 0 already,
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
and all we have to do to get a 0 where that
upper left 3 in on the top row, is to add the
numbers in the second column to the corresponding
numbers in the first column.
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
|-3+3 3 0|
-2×|-1-3 -3 -2|
| 1+5 5 1|
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
So let's cross out all the other elements in the
same row and column that that 3 is in:
|
Notice that since the 2 is in the bottom left hand
corner and there is a - in the bottom left-corner in
the sign scheme, we must change the sign of the 2, to
a -2. (If the 2 had been in a position where there is a
+ sign in the sign scheme, we would have have just kept
the sign and used 2.)
So we have:
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
Now we have to expand that determinant. So we
pick a row with the most 0's in it, and use row
and/or column operations to get all but one 0
in that row or column.
The top (red) row below already has one 0 already,
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
and all we have to do to get a 0 where that
upper left 3 in on the top row, is to add the
numbers in the second column to the corresponding
numbers in the first column.
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
|-3+3 3 0|
-2×|-1-3 -3 -2|
| 1+5 5 1|
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
So let's cross out all the other elements in the
same row and column that that 3 is in:
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
Now multiply that 3 by the 2x2 determinant formed
by the 4 numbers that haven't been crossed out,
so we have:
-2*( )3*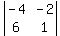 But we must now check the sign scheme to see whether
we keep the positive sign of the 3 or whether we must
change its sign to get its opposite, -3.
This is the 3x3 sign scheme.
But we must now check the sign scheme to see whether
we keep the positive sign of the 3 or whether we must
change its sign to get its opposite, -3.
This is the 3x3 sign scheme.
 Notice that since the 3 is in the middle of the top row,
and there is a + in the middle of the top row in the sign
scheme, we change the sign of the 3 to -3.
So we have
Notice that since the 3 is in the middle of the top row,
and there is a + in the middle of the top row in the sign
scheme, we change the sign of the 3 to -3.
So we have
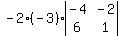 or
or
 = =
 Edwin
Edwin
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! |1 -3 2 0|
|-3 -1 0 -2|
|2 1 3 1|
|2 0 -2 0
-------------
Break it up into 4 3rd order matrices by eliminating one column at a time, and multiplying by the coefficient in the top row. Also, the sign alternates, + and minus.
1 times
|-1 0 -2|
| 1 3 1|
| 0 -2 0|
= 1 times {-1 -2}
= -1*2 -2
= -2 + 4
= 2
------------------
The 2nd sub matrix is negative
- (-3) times
|-3 0 -2|
| 2 3 1|
| 2 -2 0|
= 3 times [-3*(3*0 - (-2)*1)] -2
= 3
= 3
= 42
------------
The 3rd one is positive
2 times
|-3 -1 -2|
| 2 1 1|
| 2 0 0|
= 2 times [-3*(0) +1*(0 - 2) -2*(0 - 2)]
= 2
= 4
-----------
The 4th is zero.
The Determinant is the sum, 2+42+4 = 48.
It's an error prone calculation, which is why I made an Excel sheet that always gets it right.
|
|
|
| |