Question 154119This question is from textbook Intermediate Algebra
: Find two integers whose product is 105 such that one of the integers is one more twice the other integer.
This question is from textbook Intermediate Algebra
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find two integers whose product is 105 such that one of the integers is one more twice the other integer.
.
Let x = one of two integers
and y = second of two integers
.
Since we have two unknowns, we'll need two equations.
.
Equation 1 comes from:"whose product is 105 "
xy = 105
.
Equation 2 comes from:"one of the integers is one more twice the other integer"
x = 2y + 1
.
Using the definition of 'x' from equation 2, we substitute it into equation 1 a nd solve for 'y':
xy = 105
(2y + 1)y = 105
2y^2 + y = 105
2y^2 + y - 105 = 0
.
Since it can't easily be factored, we can use the "quadratic equation" to solve. Doing so yields (See reference below):
y = {7, -7.5}
.
If y = 7, we can find 'x' by substituting it into equation 1 and solve for 'x':
xy = 105
x(7) = 105
x = 105/7
x = 15
.
If y = -7.5
xy = 105
x(-7.5) = 105
x = 105/(-7.5)
x = -14
.
Conclusion -- there are two possible answers:
(x,y) = (15,7)
(x,y) = (-14,-7.5)
.
For reference, here is the details of the quadratic:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=841 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 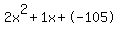 can be factored: can be factored:

Again, the answer is: 7, -7.5.
Here's your graph:
 |
|
|
|