Find the length of the major and minor axes of an ellipse with the equation
We must first get the equation in either of these two
standard forms:
or 
where a is half the length of the major axis, and where b is
half the length of the minor axis.
Rearrange to get the x terms together and the y terms togethsr.
That is, swap the middle two terms:
Factor the coefficient, 16, of 
out of the two x-terms.
Factor the coefficient, 25, of 
out of the two y-terms.
Out to the side or on scratch paper,
we complete the square of
:
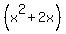1. Multiply the coefficient, 2, of 
, by 
,
getting 
.
2. Then square , getting 1
3. Add then subtract inside the first parentheses:
Now we complete the square of
:
1. Multiply the coefficient, -6, of 
, by ,
getting 
.
2. Then square , getting 9
3. Add then subtract 
inside the second parentheses:
Factor the first three terms in each parentheses:
Write as perfect squares:
Distribute the 16 and the 25, leaving the squared
expressions intact:
Combine the -16 and the -225
Add 241 to both sides:
Divide through by 400 to get a 1 on the right:
Divide top and bottom of first fraction by coeffficient 16.
Divide top and bottom of second fraction by coefficient 25.
So we compare that to
and find that 
and 
So 
and 
So half the major axis' length is 5, and the
whole major axis is 10 units in length.
Half the minor axis' length is 4, so the whole
minor axis is 8 units in length.
Edwin
