|
Question 153220: Find the solution of the system; type and ordered pair.
9x-2y=-47
8x+48=y
Please talk me through this. I have quite a few examples of how to solve it, it's just that instead of an addition sign theres a subtraction sign and it's confusing my dumb little mind.
Found 2 solutions by stanbon, Electrified_Levi:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 9x-2y=-47
8x+48=y
------------
Rearrange to use elimination:
9x - 2y = -47
8x - y = -48
-----------------
Now the objective is to have the same number of x's or y's in both equations.
So, multiply the 2nd equation by 2 and rewrite the system.
-----------------
9x - 2y = -47
16x -2y = -96
==============
Subtract the 1st equation from the 2nd to get:
7x = -49
x = -7
-----------------
Substitute into 8x+48=y to solve for "y":
y = 8*-7 + 48
y = -56 + 48
y = -7
-------------
Final solution: (-7,-7)
===============
Cheers,
Stan H.
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
Find the solution of the system; type an ordered pair.
.
9x-2y=-47
8x+48=y
.
Please talk me through this. I have quite a few examples of how to solve it, it's just that instead of an addition sign theres a subtraction sign and it's confusing my dumb little mind.
.
This is the way I usually do these kind of problems, and harder ones(3 variables, and 4 variables)
.
First, solve for a letter in each equation, since we already know what "y" is in the second equation, all we have to do is solve for "y" in the first equation
(you use the negative numbers just like positive numbers)
.
Since "y = 8x+48" in our second equation, we will solve "y" in our first equation
.

.
We will move the (-2y) over to the right, and make it positive( by adding 2y to both sides)
.

.

.
We will switch the 2y, and (-47)
.

.
We will move the (-47) over to the left side(we will add 47 to both sides)
.
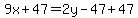
.

.

.
To solve for "y" we will now divide everything by "2"
.

.

.
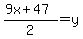
.

.
now that we found "y" in both equations
.

.

.
We can put both answers in an equation, since "y" equals both of the answers, both answers equal each other
.

.

.
We will now cross multiply to get rid of the fractions
.

.
We will use distribution
.

.
We will move (9x) over to the right side(by subtracting 9x from both sides)
.

.

.

.
We will move "96" to the left side(by subtracting 96 from both sides)
.

.

.

.
We will divide each side by "7" to solve "x"
.

.

.

.

.
We found that "x" = (-7), we will replace "x" with (-7) in one of our original equations, we will use the second equation
.
 = = 
.
 = = 
.

.

.
We found that "y" = (-8), we can replace "x", and "y", with the numbers in our first equation to check our answers
.
x = (-7)
y = (-8)
.
 = = 
.
 = = 
.
 = = 
.
 = = 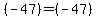
.
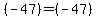 (True) (True)
.
x = (-7)
y = (-8)
.
The ordered pair is equal to (x,y), our ordered pair = (-7,-8)
.
So if it is a negative number/variable, like ( x - y = 0), you add the number/variable to both sides, (x - y + y = 0 + y), it becomes
(x = y)
.
If it is a positive number/variable, like ( x + y = 0), you subtract the number/variable from both sides, (x+y-y = 0-y), it becomes
(x=(-y))
.
Your answers are
.
x = (-7)
y = (-8)
.
Ordered Pair = (-7,-8)
.
Hope I helped, Levi
|
|
|
| |