Question 15307: find the domain and range of the function
f(x)= xsquared-x
Answer by wgunther(43)   (Show Source): (Show Source):
You can put this solution on YOUR website! Domain is the numbers you are allowed to plug in as input. Range is the numbers you can get out of it.

The domain is anything, right? Because we can plug any x we want to into that equation and it would be anthing funky, like a negative even root or a zero in the denominator. So, we could say the answer is R, the set of all real numbers, or (-inf, inf) if you wanted it in interval notation.
As for range, what are the numbers that x^2-x be? Sometime we're tempted to say all numbers, because the domain is all numbers, but that's not the case here. If you graph it, you can easily see the range.
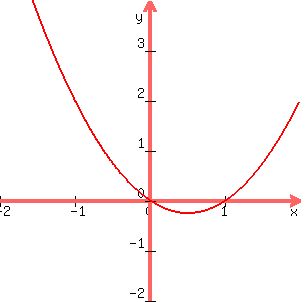
For quadratic functions, the range will never be (inf,inf) because there's always a vertex, or a maxiumum or minimum. Here there is a minimum. If you put the quadratic in vertex form:



There we see the vertex is at (1/2,-1/4), therefore the minimum y value is -1/4. So, we can say the range is [-1/4,inf) in interval notation, or the set of all numbers where 
|
|
|