|
Question 153051: Please explain how to reverse FOIL when factoring a polynomial of the form ax(squared) + bx + c when a = 1 and when a does not = 1.
Found 2 solutions by stanbon, Fombitz:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Example:
If a = 1
--------
x^2 + 5x + 6
The procedure is called "the AC Method".
1st: think of two numbers whose product is AC = 1*6 = 6
and whose sum is B = 5
--------
The numbers are 2 and 3
--------
2nd: Replace the B-term by the sum you have found:
x^2 _+ 2x + 3x + 6
----------
3rd: Factor and 1st two and the last two terms separately:
x(x+2) + 3(x+2)
----------
4th: Factor again to get the answer:
(x+2)(x+3
-------------------------------------------------
Example:
a not equal to 1
2x^2 - x - 21
1st: think of two numbers whose product is AC = 2*21 = 42
and whose sum is B = -1
---------------
The numbers are -7 and 6
---------------
2nd: replace the B-term with the sum you found:
2x^2 -7x+6x -21
----------
3rd: factor the 1st two and the last two terms separately:
x(2x-7) +3(2x-7)
--------
4th: Facor again
(2x-7)(x+3)
==================
Cheers,
Stan H.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a general quadratic equation using FOIL,


As you can see it can be complicated.
Typically a=1, so you can make the assumption that d=f=1.
This is not always true because you could have d=2 and f=1/2, then a=df=1.
When a is not 1, then it becomes more difficult because there are more choices to check.
.
.
.
Best bet is always start at c and look for its factors, e and g.
If a=1 it becomes easier.
The middle term (the x term) is just e+g.
If a does not equal 1, you can still do it but your number of guesses increases until you hit that right combination of d,e,f,g.
.
.
.
Best bet is to become more familiar with combinations of numbers multiplied together and then added.
As an example, take 5 and 8.
Let's not worry if they're positive or negative.
Multiplied, they're 40(-40).
If they're added or subtracted you could get (-13,-3,3,13)
So from 5 and 8 you can get




.
.
.
If you look at the case where a is not equal 1, it can be more tricky,




Best bet is always start with the easiest possible solution guess,
If a=3 then start with
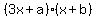
If a=4, then the simplest choices would be,

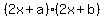
As you can see if a has a lot of factors the number of choices grows quickly.
It can be tedious but there are only a limited number of possibilities.
Good luck.
|
|
|
| |