Question 153019: 1. Suppose you use five different letters to make a computer password. Find the number of possible five letter passwords.
I got 11,881,376 using the formula 26 C 5. Is this correct?
2. How many different ways can someone arrange 8 books on a shelf? I got 64.
3. If the first three digits of someone's phone number (no area code) are 555, how many different phone numbers could they have? I got 11,881,373
I used 26 to the 5th power.
Thanks for your help.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) Here's a good question: is the password "pass" different from "ssap"? Since it is, this means that order matters.
Since order does matter, we must use the permutation formula:
  Start with the permutation formula Start with the permutation formula
 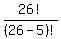 Plug in Plug in  and and 
 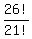 Subtract Subtract 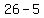 to get 21 to get 21
Expand 26!
 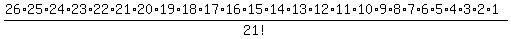
Expand 21!
 
  Cancel Cancel
 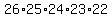 Simplify Simplify
 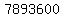 Now multiply 26*25*24*23*22 to get 7,893,600 Now multiply 26*25*24*23*22 to get 7,893,600
So there are 7,893,600 possible passwords
2)
If order does matter, then the number of combinations is 
So there are 40,320 ways to rearrange the books
3)
Let's say that the format is
(555)-xxx-xxxx
So we have 7 slots we're dealing with. This means that  . Since we have 10 numbers to choose from, this tells us that . Since we have 10 numbers to choose from, this tells us that  (note: the "26" that you used implies that you'll be using letters). Also, because order matters, we must use the permutation formula: (note: the "26" that you used implies that you'll be using letters). Also, because order matters, we must use the permutation formula:
  Start with the permutation formula Start with the permutation formula
 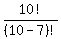 Plug in Plug in  and and 
 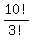 Subtract Subtract  to get 3 to get 3
Expand 10!
 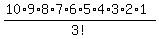
Expand 3!
 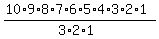
 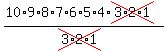 Cancel Cancel
  Simplify Simplify
 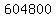 Now multiply 10*9*8*7*6*5*4 to get 604,800 Now multiply 10*9*8*7*6*5*4 to get 604,800
So there are 604,800 unique phone numbers to choose from.
|
|
|