Question 152862: Consider polynomial  ; what is its maximum number of zeroes? @ The maximum number of zeroes = n, regardless of the value of n. ; what is its maximum number of zeroes? @ The maximum number of zeroes = n, regardless of the value of n.
a. 0
b. 1
c. Cannot be determined without first knowing the value of n
d. None of the above
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider polynomial  ; what is its maximum number of zeroes? @ The maximum number of zeroes = n, regardless of the value of n. ; what is its maximum number of zeroes? @ The maximum number of zeroes = n, regardless of the value of n.
a. 0
b. 1
c. Cannot be determined without first knowing the value of n
d. None of the above
We apply Descartes' rule of signs, which says:
If f(x) = a polynomial in descending order, then:
1. The maximum number of positive zeros of polynomial f(x),
is the number of sign changes in f(x), going left to right.
2. The maximum number of negative zeros of polynomial f(x),
is the number of sign changes in f(-x), going left to right.
 has only two terms, and NO sign changes. Therefore it has NO
POSITIVE zeros.
Now let's test it for NEGATIVE zeros.
We form
has only two terms, and NO sign changes. Therefore it has NO
POSITIVE zeros.
Now let's test it for NEGATIVE zeros.
We form 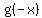 by replacing by replacing  by by  . .
 Now since we do not know whether n is even or odd, we have to
consider both cases:
If
Now since we do not know whether n is even or odd, we have to
consider both cases:
If  is even, then is even, then 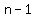 is odd, so is odd, so  and and
 So in this case
So in this case
 That has 1 sign change, so g(x) would have a maximum of 1 negative zero.
----------
If
That has 1 sign change, so g(x) would have a maximum of 1 negative zero.
----------
If  is odd, then is odd, then 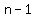 is even, so is even, so  and and
 So in this case
So in this case
 That also has 1 sign change, so g(x) would have a maximum of 1
negative zero regardless of whether n is even or odd.
---------
Now we know that it has no positive zeros, a maximium of
1 negative zero.
However we must also check to see if 0, which is neither
positive nor negative, is a zero. So we find
That also has 1 sign change, so g(x) would have a maximum of 1
negative zero regardless of whether n is even or odd.
---------
Now we know that it has no positive zeros, a maximium of
1 negative zero.
However we must also check to see if 0, which is neither
positive nor negative, is a zero. So we find 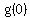


 Therefore 0 is also a zero, regardless of n.
So the maximium number of zeros is 2.
Since 2 is not listed as a choice, then the only correct
choice is d "None of the above".
--------------
Comment:
It's easy to see the correct choice cannot be 0 or 1
because when
Therefore 0 is also a zero, regardless of n.
So the maximium number of zeros is 2.
Since 2 is not listed as a choice, then the only correct
choice is d "None of the above".
--------------
Comment:
It's easy to see the correct choice cannot be 0 or 1
because when 

 This has two zeros 0 and -4.
And we showed above that c cannot be the answer,
for we were able to determine that the maximum number
of zeros is 2.
Edwin
This has two zeros 0 and -4.
And we showed above that c cannot be the answer,
for we were able to determine that the maximum number
of zeros is 2.
Edwin
|
|
|