Question 152808: solve the system:
x+3y+5z=20
y-4z=-16
3x-2y+9z=36
Answer by Electrified_Levi(103)   (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
solve the system:
.
x+3y+5z=20
y-4z=(-16)
3x-2y+9z=36
.
This is the way I usually solve these problems(pretty easy once you know how to do it) ( There is no fast way to solve these problems)
.
First, solve for a letter in all the equations( since we already have a 2 system/variable equation for equation 2, we don't have to solve for any letter in equation 2)( Since  that means we will need to solve for "x" in our other equations)
.
We will rewrite the 3 equations so it makes more sense( the second equation has no "x's" in the equation so it has "0x")
.
x+3y+5z=20
0x + y - 4z =( -16)
3x-2y+9z=36
.
We will switch the equations around
.
x+3y+5z=20
3x-2y+9z=36
0x + y - 4z = (-16)
.
We will solve "x" in our first two equations(can't solve "x" in our third equation, since it is 0x)
.
First equation
.
.
We will move "3y" over to the right side
.
= 
.
= 
.
We will move "5z" to the right side
.
= 
.
= 
.
We will switch the letters around
.
= 
.
This is our First Answer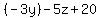 
.
We will now solve "x" in our second equation
.
.
We will move (-2y) to the right side
.
= 
.
= 
.
We will move "9z" to the right side
.
= 
.
= 
.
We will switch the letters around
.
= 
.
We will now divide each side by "3"
.
= 
.
= 
.
.
Our second answer =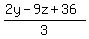 
.
We can now solve to get a 2 system(variable) equation
.
We will put our two answers together in an equation, since "x" = both of the answers, our answers equal each other
.
First answer =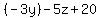
.
Second answer =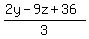
.
Our equation will equal 
.
= 
.
We will use cross multiplication to get rid of the fractions
.
.
.
We will move (-9y) to the right side
.
.
= 
.
We will move the (-15z) to the right side
.
= 
.
= 
.
We will move the "36" to the left side
.
= 
.
= 
.
We will rearrange, = 
.
Our second 2 system/variable equation =
.
We will put our two 2 system/variable equations side by side
.
First equation = 
.
Second equation =
.
.
.
We will now need to solve for a letter again( we will solve "y" since it is the easiest to solve)
.
First equation
.
We will move (-4z) to the right side
.
= 
.
= 
.
=  ( rearranging the numbers)
.
Our first answer =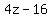 
.
Our second equation
.
We will move "6z" to the right side
.
= 
.
= 
.
Rearranging = 
.
We will divide each side by "11"
.
= 
.
= 
.
= 
.
Our second answer is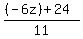 
.
We can now put both of our answers into an equation( since "y" equals both of our answers)
.
Answer 1 =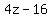
.
Answer 2 =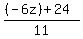
.
We can make our equation, it equals 
.
= 
.
We will cross multiply to get rid of the fractions
.
.
It becomes, 
.
We will move (-6z) to the left side
.
= 
.
= 
.
We will move (-176) to the right side
.
= 
.
= 
.
We will divide each side by "50"
.
= 
.
= 
.
= 
.
We found that "z" = 4, we can replace "z" with "4" in one of our 2 system/variable equations
.
.
.
We will use the first equation
.
= 
.
= 
.
We will move (-16) to the right
.
= 
.
= 
.
We found that "y" = "0"
.
We can now find "x", we need to replace "y" and "z" in one of the three original equations
.
y = 0
z = 4
.
x+3y+5z=20
y-4z=(-16)
3x-2y+9z=36
.
We will use the first equation, since it will be the easiest( we can't use the second equation)
.
= 
.
= 
.
= 
.
We will move the "20" over to the right side
.
= 
.
.
We found that "x" = "0", we now have all 3 variables, "x","y", and "z"
.
x = 0
y = 0
z = 4
.
We can check by replacing the letters with numbers in our third equation
.
= 
.
= 
.
=  ( True)
.
x = 0
y = 0
z = 4
.
The solution set = (x,y,z), our solution set = (0,0,4)
.
Hope I helped, Levi
|
|
|
