SOLUTION: {{{(A-1)/(A+1)+(A+1)/(A-1)}}}

Algebra ->  Rational-functions -> SOLUTION: {{{(A-1)/(A+1)+(A+1)/(A-1)}}}      Log On


   

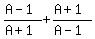
Question 152788: %28A-1%29%2F%28A%2B1%29%2B%28A%2B1%29%2F%28A-1%29
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
%28A-1%29%2F%28A%2B1%29%2B%28A%2B1%29%2F%28A-1%29

Put parentheses around all the numerators and
denominators:

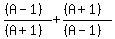%28%28A-1%29%29%2F%28%28A%2B1%29%29%2B%28%28A%2B1%29%29%2F%28%28A-1%29%29

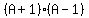The LCD is %28A%2B1%29%28A-1%29

The first fraction's denominator needs a
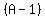factor of %28A-1%29 to become the LCD.
So we multiply top and bottom of the first
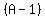fraction by %28A-1%29:

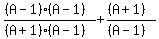%28%28A-1%29%28A-1%29%29%2F%28%28A%2B1%29%28A-1%29%29%2B%28%28A%2B1%29%29%2F%28%28A-1%29%29

The second fraction's denominator needs a
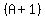factor of %28A%2B1%29 to become the LCD.
So we multiply top and bottom of the second
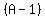fraction by %28A-1%29:



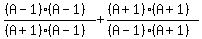FOIL out the tops but DO NOT FOIL out the bottoms!

[Note: Sometimes it doesn't matter if you FOIL out the
bottoms, but it is better not to because sometimes
it turns out that after simplifying the tops, one of
the factors in the denominator will happen to cancel
with one of the factors in the numerator, so to be on
the safe side, do not multiply out the bottoms, but
only multiply out the tops.]




Since the denominators are equal, we can combine the numerators
over the common denominator:

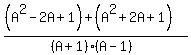%28%28A%5E2-2A%2B1%29%2B%28A%5E2%2B2A%2B1%29%29%2F%28%28A%2B1%29%28A-1%29%29%29

Remove the parentheses in the top:

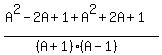%28A%5E2-2A%2B1%2BA%5E2%2B2A%2B1%29%2F%28%28A%2B1%29%28A-1%29%29%29

Combine terms in the top:

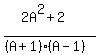%282A%5E2%2B2%29%2F%28%28A%2B1%29%28A-1%29%29%29

Factor 2 out of the top:

%282%28A%5E2%2B1%29%29%2F%28%28A%2B1%29%28A-1%29%29%29

It turns out that nothing will cancel, so if
you like, now you can multiply everything
out:

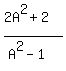%282A%5E2%2B2%29%2F%28A%5E2-1%29%29

Edwin