Question 152652: Which of the following is a reflection of f(x) = -x + 1 about the x-axis?
r(x) = x + 1
r(x) = x - 1
r(x) = -( x - 1)
None of the above
Answer by mducky2(62)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's sketch f(x) = -x + 1. All linear equations can be represented as f(x) = mx + b. The m is the slope of the line. We know it has the same slope. Therefore, the graph above will have the same slope as f(x) = -x + 1.
The b is the y-intercept at the point (0,b). In this case, b = 1. So we know it intersects the y-axis at the point (0,1):

Now let's try to figure out what the reflection looks like. In order to be a reflection of f(x) = -x + 1, it should have the opposite slope and opposite y-intercept.
Since the slope of the original function is m = -1, the opposite slope would be m = 1.
Since the intercept is one unit above the x-axis, the next time, it should be one unit below. That would be at the point (0,-1) or b = -1.
Putting that all together:
r(x) = mx + b
r(x) = (1)x + (-1)
r(x) = x - 1
Graphing that equation:
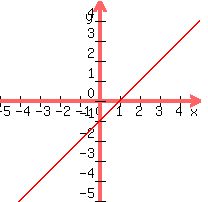
Now let's graph both equations to make sure they are reflections of each other:

They are reflections of each other. Therefore, the answer is r(x) = x - 1.
|
|
|