Question 152346This question is from textbook
: How do you find the slope with only one point to work with? The first point is (3,4). The problem I am trying to solve is: Consider the semicircle of radius 5 centered at (0,0) as shown in the figure. Find an equation of the line tangent to the semicircle at the point (3,4). (hint: A line tangent to a circle is perpendicular to the radius at the point of tangency.)
This question is from textbook
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't see the figure you allude to but it's easy enough imagine what it looks like.
In your semicircle, consider the radius from the center to the point of tangency (3, 4). This radius has a slope of  (rise = 4 over run = 3). Now any line that is perpendicular to this radius. eg, the tangent line at (3, 4), will have a slope that is the negative reciprocal of the slope of this radius. So the slope of the tangent line will be (rise = 4 over run = 3). Now any line that is perpendicular to this radius. eg, the tangent line at (3, 4), will have a slope that is the negative reciprocal of the slope of this radius. So the slope of the tangent line will be 
So now you can write:
 But of course, you still need to find the value of b, the y-intercept, so substitute the x- and y-coordinate values of the point of tangency (3, 4) into this equation and solve for b. But of course, you still need to find the value of b, the y-intercept, so substitute the x- and y-coordinate values of the point of tangency (3, 4) into this equation and solve for b.
 Substitute x = 3 and y = 4 Substitute x = 3 and y = 4
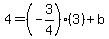 Solve for b. Solve for b.


So your final equation would be:
 or, if you multiply through by 4 to clear the fractions, it becomes: or, if you multiply through by 4 to clear the fractions, it becomes:

|
|
|