|
Question 152218:
evaluate the determinant:
| 1 -3 2 0|
|-3 -1 0 -2|
| 2 1 3 1|
| 2 0 -2 0|
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
evaluate the determinant:
| 1 -3 2 0|
|-3 -1 0 -2|
| 2 1 3 1|
| 2 0 -2 0|
Pick a row with the most 0's in it, and
use row and/or column operations to get all
but one 0 in that row or column.
The red row below already has two 0's,
| 1 -3 2 0|
|-3 -1 0 -2|
| 2 1 3 1|
| 2 0 -2 0|
and all we have to do to get a 0 where that
red -2 is on the bottom row, is to add the
numbers in the first column to the corresponding
numbers in the third column. We get this:
| 1 -3 2+1 0|
|-3 -1 0-3 -2|
| 2 1 3+2 1|
| 2 0 -2+2 0|
or
| 1 -3 3 0|
|-3 -1 -3 -2|
| 2 1 5 1|
| 2 0 0 0|
Now all the numbers on the bottom row are 0's
all except for one, the 2 in the lower left
corner.
So let's cross out all the other elements in the
same row and column that that 2 is in:
| 1 -3 3 0|
|-3 -1 -3 -2|
| 2 1 5 1|
| 2 0 0 0|
Now multiply that 2 by the 3x3 determinant formed
by the 9 numbers in the upper right:
|-3 3 0|
( )2×|-1 -3 -2|
| 1 5 1|
But we must now check the sign scheme to see whether
we keep the positive sign of the 2 or whether we must
change its sign to get its opposite, -2.
This is the sign scheme for the 4x4 determinant.
 Notice that since the 2 is in the bottom left hand
corner and there is a - in the bottom left-corner in
the sign scheme, we must change the sign of the 2, to
a -2. (If the 2 had been in a position where there is a
+ sign in the sign scheme, we would have have just kept
the sign and used 2.)
So we have:
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
Now we have to expand that determinant. So we
pick a row with the most 0's in it, and use row
and/or column operations to get all but one 0
in that row or column.
The top (red) row below already has one 0 already,
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
and all we have to do to get a 0 where that
upper left 3 in on the top row, is to add the
numbers in the second column to the corresponding
numbers in the first column.
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
|-3+3 3 0|
-2×|-1-3 -3 -2|
| 1+5 5 1|
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
So let's cross out all the other elements in the
same row and column that that 3 is in:
|
Notice that since the 2 is in the bottom left hand
corner and there is a - in the bottom left-corner in
the sign scheme, we must change the sign of the 2, to
a -2. (If the 2 had been in a position where there is a
+ sign in the sign scheme, we would have have just kept
the sign and used 2.)
So we have:
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
Now we have to expand that determinant. So we
pick a row with the most 0's in it, and use row
and/or column operations to get all but one 0
in that row or column.
The top (red) row below already has one 0 already,
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
and all we have to do to get a 0 where that
upper left 3 in on the top row, is to add the
numbers in the second column to the corresponding
numbers in the first column.
|-3 3 0|
-2×|-1 -3 -2|
| 1 5 1|
|-3+3 3 0|
-2×|-1-3 -3 -2|
| 1+5 5 1|
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
So let's cross out all the other elements in the
same row and column that that 3 is in:
| 0 3 0|
-2×|-4 -3 -2|
| 6 5 1|
Now multiply that 3 by the 2x2 determinant formed
by the 4 numbers that haven't been crossed out,
so we have:
-2*( )3*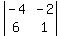 But we must now check the sign scheme to see whether
we keep the positive sign of the 3 or whether we must
change its sign to get its opposite, -3.
This is the 3x3 sign scheme.
But we must now check the sign scheme to see whether
we keep the positive sign of the 3 or whether we must
change its sign to get its opposite, -3.
This is the 3x3 sign scheme.
 Notice that since the 3 is in the middle of the top row,
and there is a + in the middle of the top row in the sign
scheme, we change the sign of the 3 to -3.
So we have
Notice that since the 3 is in the middle of the top row,
and there is a + in the middle of the top row in the sign
scheme, we change the sign of the 3 to -3.
So we have
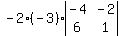 or
or
 = =
 Edwin
Edwin
|
|
|
| |