Question 151779: Hello, please explain to me how I should set up a system of equations to solve this problem. How many liters of a 30% acid solution must be added to a 10% acid solution to obtain 32 liters of a 15% acid solution?
Found 2 solutions by vleith, jojo14344:
Answer by vleith(2983)   (Show Source):
Answer by jojo14344(1513) (Show Source):
You can put this solution on YOUR website! We respect everybody here but there's no harm in trying this one:
Remember the following:
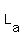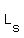 = liters of acid = unknown????
 = liters of solution = unknown???
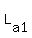 = final stage of acid when mixed w/ solution
Now, we all know when we add the volume of 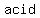 &  we get 32 Liters. To show:
 -----------------> eqn 1
Now, "percent of concentration" makes the difference on how many "Liters" of acid we need to put. Putting this into eqn,
 ------------> working eqn
In summary of the working eqn, 30% of Liters of acid + 10% of Liters of solution equals 15% of 32 Liters of the NEW acid solution.
.
In eqn 1 we get,  and substitute in our working eqn:
 ---------------> amount of Acid Solution that must be added.
FOR THE AMOUNT of SOLUTION, go back eqn 1,
 , 
 --------------> amount of SOLUTION that must be added.
Besides,
Thank you,
Jojo
|
|
|
