Could you please help me solve this system of equations by using 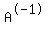 ?
?
x+5y+5z=-7
x+4y+5z=-5
x+5y+4z=-5
We form the matrix equation  where
where
 ,
,  ,
,  So the matrix equation is
So the matrix equation is  or
A * X = B
or
A * X = B
 Do you know how to find the inverse of a matrix?
If not post again asking how. The inverse of
matrix A is:
Do you know how to find the inverse of a matrix?
If not post again asking how. The inverse of
matrix A is:
 So we left-multiply both sides of the equation by this
inverse matrix,
So we left-multiply both sides of the equation by this
inverse matrix, 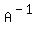
 Do you know how to multiply matrices? If not
post again asking how.
Multiply the matrices and get this:
Do you know how to multiply matrices? If not
post again asking how.
Multiply the matrices and get this:

 So
So  ,
,  ,
,  Edwin
Edwin