Question 15127: A^T denotes the transpose of a matrix A.
Show that = Tr(B^T,A) defines an inner product on R^(n x n)
Let U be the set of symmetric 2 x 2 matrices with real entries. U is subspace of R (2x2). Find an orthonormal basis of U with respect to the above inner product.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! A : nxn square matrix over R. (missing)
A^T denotes the transpose of a matrix A.
Show that = Tr(B^T,A) defines an inner product on 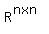
Let U be the set of symmetric 2 x 2 matrices with real entries. U is subspace of R (2x2). Find an orthonormal basis of U with respect to the above inner product.
Let A = (aij), B = (bij) be nxn sq. matrices over R. (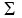 means summation) means summation)
Define (A,B) = 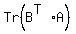 = = 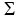 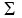 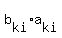 (k=1,2..,n)(i=1,2..,n) (k=1,2..,n)(i=1,2..,n)
You have to check the definition of inner product (as symmetric
, linear, positive definite, all very easy)
Note the dim of the vector space  = 4. = 4.
And dim U = 3 (why?)
Let A=
(1 0)
(0 0)
B=
(0 0)
(0 1)
C =
(0 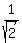 ) )
( 0) 0)
then {A,B,C} forms an o.n. basis of U.
You should test (A,A)=(B,B)=(C,C)= 1.
(A,B) = (B,C) =(C,A) = 0
Kenny
|
|
|