Question 151018: A RECTANGLE IS 4 TIMES AS LONG AS IT IS WIDE A SECOND RECTANGLE IS 5 CENTIMETERS LONGER AND 2 CENTIMETERS WIDER THAN THE FIRST. THE AREA OF THE SECOND RECTANGLE IS 270 SQUARE CENTIMETERS GREATER THAN THE FIRST. WHAT ARE THE DIMENSIONS OF THE ORIGINAL RECTANGLE
Answer by jojo14344(1513)   (Show Source): (Show Source):
You can put this solution on YOUR website! We need to remember the following,
1st rectangle (original) 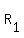 is designated below, is designated below,
 , ,  , & , & 
2nd rectangle, 
 , ,  , & , & 
In 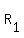 : :  ---> length 4 times its width ---> length 4 times its width
So,  ---> --->  ----------> eqn 1 ----------> eqn 1
.
In  : :  ---> 5 cm longer ---> 5 cm longer
Also,  ----------> 2 cm wider ----------> 2 cm wider
So,  -------------------------------------------->A -------------------------------------------->A
And we have to remember,  ---> greater than 270sqcm-->B ---> greater than 270sqcm-->B
Plug in eqn 1 in this condition:  ---------------->C ---------------->C
Therefore, equating A & C,

Remember in 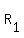 that that  & substitute: & substitute:


 ------> ------> ---> --->  ---> ORIG. WIDTH ---> ORIG. WIDTH
We know  ------------> ------------>  ----> ORIG LENGTH ----> ORIG LENGTH
.
For checking & verification,


This satisfy condition B above ----->  is 270cm greater than is 270cm greater than 
1870-1600=270cm
Thank you,
Jojo
|
|
|