Question 151000: A basketball fieldhouse seats 15,000. Courtside seats sell for $ 9, endzone for $7, and balcony for $4. The total revenue from a sell-out is $81,000. If half the courtside and balcony seats and all the endzone seats are sold, the total revenue is $47,500. How many of each type are there?
Found 2 solutions by mducky2, ankor@dixie-net.com:
Answer by mducky2(62)   (Show Source): (Show Source):
You can put this solution on YOUR website! Because there are three unknowns (courtside, endzone, and balcony seats), there have to be a minimum of three equations to solve it.
You know the total number of seats, so you can set up the equation:
c + e + b = 15000
We'll call this equation A.
You also know the total revenue when all the seats are sold out, plus the prices of each of the seats, so you can set up the equation:
9c + 7e + 4b = 81000
We'll call this equation B.
The problem also tells you the revenue when only half the courtside and balcony seats are sold and when all the endzone seats are sold, giving the equation:
½(9c) + 7e + ½(4b) = 47500
(9/2)c + 7e + 2b = 47500
We'll call this equation C.
When you have three equations, in order to solve them, try to add and subtract them from each other so that you end up with only two equations and two variables. Looking at the above equations, it looks like it would be easier to solve for c and b. Equation B minus equation C would eliminate e.
9c + 7e + 4b = 81000
-[(9/2)c + 7e + 2b = 47500]
---------------------------------
(9/2)c + 2b = 33500
Equation B minus seven times equation A will also eliminate e while leaving b and c behind:
9c + 7e + 4b = 81000
- 7[c + e + b] = 7 * 15000
---------------------------
2c - 3b = -24000
Choose a variable in both equations and solve for it. We will solve for b.
(9/2)c + 2b = 33500
2b = 33500 - (9/2)c
b = 16750 - (9/4)c
2c - 3b = -24000
2c + 24000 = 3b
b = (2/3)c + 24000/3
b = (2/3)c + 8000
Now you can combine the equations:
16750 - (9/4)c = b = (2/3)c + 8000
16750 - 8000 = (2/3)c + (9/4)c
8750 = (8/12)c + (27/12)c
8750 = (35/12)c
c = 3000
Plug this into one of the smaller equations:
b = (2/3)c + 8000
b = (2/3)(3000) + 8000
b = 2000 + 8000
b = 10000
Now you can plug this into one of the original equations. Equation A looks easiest:
c + e + b = 15000
e = 15000 - c - b
e = 15000 - 3000 - 10000
e = 2000
Therefore, the stadium has 3000 courtside seats, 2000 endzone seats, and 10000 balcony seats.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A basketball fieldhouse seats 15,000. Courtside seats sell for $ 9, endzone for $7, and balcony for $4. The total revenue from a sell-out is $81,000. If half the courtside and balcony seats and all the endzone seats are sold, the total revenue is $47,500. How many of each type are there?
:
c = no. of courtside seats
e = no. of endzone seats
b = no. of balcony seats
:
Write a total seats equation:
c + e + b = 15000
:
Write an equation reflecting a sell-out:
9c + 7e + 4b = 81000
;
Write an equation for the statement:
"If half the courtside and balcony seats and all the endzone seats are sold, the total revenue is $47,500."
9(.5c) + 7e + 4(.5b) = 47500
which is:
4.5c + 7e + 2b = 47500
;
Using the above equation with the sell-out equation, eliminates e"
9c + 7e + 4b = 81000
4.5c+ 7e + 2b = 47500
-----------------------subtraction eliminates e:
4.5c + 2b = 33500
:
Multiply the total seats equation by 7 and subtract from the sellout equation
9c + 7e + 4b = 81000
7c + 7e + 7b = 105000
----------------------- subtraction eliminates e
2c - 3b = -24000
;
Two equations, two unknowns, we should be able to handle this now
:
Multiply the 1st one by 3, and the 2nd one by 2; resulting in:
13.5c + 6b = 100500
4c - 6b = -48000
---------------------- addition eliminates b
17.5c = 52500
c = 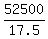
c = 3000 courtside seats
:
Find b using; 4.5c + 2b = 33500
4.5(3000) + 2b = 33500
13500 + 2b = 33500
2b = 33500 - 13500
2b = 20000
b = 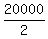
b = 10000 balcony seats
;
I'll let you find the number of endzone seats
|
|
|