Question 150527: Form a polynomial f(x) with real coefficients having the given degree and zeros.
Degree: 18; Zeros: 3 and 1+i. I know that the other zero has to be 1-i, however, I seem to have misplaced my notes from class and my textbook is not offering much help. Any assistance would be greatly appreciated. Thanks.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Are you sure that the polynomial is not of degree 3? If it's degree 18, then what is the multiplicity of each root?
So I'm going to assume that the polynomial is of degree 3.
Since  , , 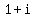 , and , and 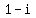 are given zeros this means that: are given zeros this means that:
 , ,  , and , and 
Get all terms to the left side in each case
 , ,  , and , and 
 Now use the zero product property in reverse to join the factors. Now use the zero product property in reverse to join the factors.
 Regroup the terms Regroup the terms
 Factor Factor 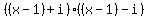 to get to get  by use of the difference of squares. Note: let by use of the difference of squares. Note: let  and rewrite the problem into and rewrite the problem into 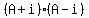
 Rewrite Rewrite  as as 
 Rewrite Rewrite 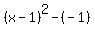 as as 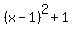
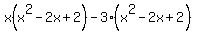 Expand. Remember, Expand. Remember, 
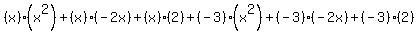 Distribute. Distribute.
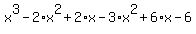 Multiply. Multiply.
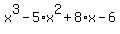 Now combine like terms. Now combine like terms.
So the polynomial of degree 3 that has the roots  , , 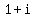 , and , and 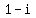 is is 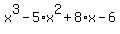
Notice how if we graph  , we can visually verify our answer (note: in this case, we can only verify the root , we can visually verify our answer (note: in this case, we can only verify the root  ) )
 Graph of Graph of  with root of with root of 
|
|
|