Question 150386: Oh dear God please help me!!! We are studying Graphs of Exponential and Logarithmic Functions and I am so lost I'm about to send out the hound dogs, but seriously if someone could please help just get me started I would greatly appreciate it.
I am supposed to Plot the graphs of the following functions:I don't understand how
1. f(x) = 7x this x variable is actually an exponent so it is 7 to the x power
2. f(x) = 4x - 3 the x-3 here is also an exponent so it reads 4 to the x-3 power
3. f(x) = (1/5)x this is actually 1/5 to the x power again the x is an exponent
4. f(x) = log3x
Thank you guys for always helping me out. I can't wait till I get this degree so I can help yall out with some $$$.
Found 2 solutions by jim_thompson5910, scott8148:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'll do the first two to get you started.
# 1
Table of Contents:
Table
Graph
In order to graph  , we need to plot a few points. , we need to plot a few points.
Let's find the y value when  note: you can start at any x value. note: you can start at any x value.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Rewrite Rewrite  as as 
 Evaluate Evaluate  to get 49 to get 49
 Divide and simplify. Divide and simplify.
So when  , ,  . So we have the point (-2,0.02). . So we have the point (-2,0.02).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Rewrite Rewrite  as as 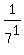
 Evaluate Evaluate 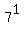 to get 7 to get 7
 Divide and simplify. Divide and simplify.
So when  , ,  . So we have the point (-1,0.143). . So we have the point (-1,0.143).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Evaluate Evaluate  to get 1 to get 1
So when  , ,  . So we have the point (0,1). . So we have the point (0,1).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Evaluate Evaluate 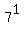 to get 7 to get 7
So when  , ,  . So we have the point (1,7). . So we have the point (1,7).
----------------------------
Now let's make a table of the values we just found.
Jump to Table of Contents
Table of Values:
| x | y | TEST: -2
| -2 | 0.02 |
| -1 | 0.143 |
| 0 | 1 |
| 1 | 7 |
Now let's plot these points:

Jump to Table of Contents
Graph:
Now draw a curve through all of the points to graph  : :
 Graph of Graph of 
# 2
Table of Contents:
Table
Graph
In order to graph  , we need to plot a few points. , we need to plot a few points.
Let's find the y value when  note: you can start at any x value. note: you can start at any x value.
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Subtract Subtract
 Rewrite Rewrite 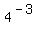 as as 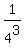
 Evaluate Evaluate  to get to get 
 Divide and simplify. Divide and simplify.
So when  , ,  . So we have the point (0,0.016). . So we have the point (0,0.016).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Subtract Subtract
 Rewrite Rewrite 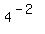 as as 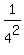
 Evaluate Evaluate  to get to get 
 Divide and simplify. Divide and simplify.
So when  , ,  . So we have the point (1,0.063). . So we have the point (1,0.063).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Subtract Subtract
 Rewrite Rewrite 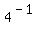 as as 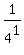
 Evaluate Evaluate 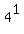 to get to get 
 Divide and simplify. Divide and simplify.
So when  , ,  . So we have the point (2,0.25). . So we have the point (2,0.25).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Subtract Subtract
 Evaluate Evaluate  to get to get 
So when  , ,  . So we have the point (3,1). . So we have the point (3,1).
----------------------------
Let's find the y value when 
 Start with the given equation. Start with the given equation.
 Plug in Plug in  . .
 Subtract Subtract
 Evaluate Evaluate 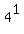 to get to get 
So when  , ,  . So we have the point (4,4). . So we have the point (4,4).
----------------------------
Now let's make a table of the values we just found.
Jump to Table of Contents
Table of Values:
| x | y | TEST: 0
| 0 | 0.016 |
| 1 | 0.063 |
| 2 | 0.25 |
| 3 | 1 |
| 4 | 4 |
Now let's plot these points:

Jump to Table of Contents
Graph:
Now draw a curve through all of the points to graph  : :
 Graph of Graph of 
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! $$$, huh...WOW!!
plotting the graphs is straight forward (a graphing calculator would be a big help)
__ the f(x) values are on the vertical (y) axis and the x values are on the horizontal axis
__ find the f(x) values by "plugging in" values for x
1. f(x)=7^x __ when x=0, f(x)=1 (this is the y-intercept) __ when x is 1, f(x)=7
__ as x becomes a large NEGATIVE value, f(x) approaches zero (horizontal asymptote)
2. f(x)=4^(x-3) __ when x=3, the exponent is 0 so f(x)=1 __ when x=0, f(x)=4^(-3) or 1/64
__ same general shape as #1 with different y-intercept
3. f(x)=(1/5)^x __ when x=0, f(x)=1
__ as x becomes a large POSITIVE value, f(x) approaches zero (horizontal asymptote)
__ this graph is sort of a "mirror image" of #'s 1 and 2
4. logarithms are NOT defined for negative quantities, so this graph is only on the right-hand side of the vertical axis
__ as x approaches zero (very small fractions), f(x) approaches negative infinity (vertical asymptote)
|
|
|