|
Question 150241: Pipe A fills a 50-liter tank at a rate of 15 liters per hour. Pipe B fills the same tank at a rate of 10 liters per hour. Pipe A runs alone for 100 minutes then the two of them together finish filling up the tank. How long does the whole operation take?
The answer is 160 minutes, but I have no idea how to arrive at this answer. Thank you!
Answer by jojo14344(1513)   (Show Source):
You can put this solution on YOUR website! The answer is right, 160 minutes.
We'll look how it arrived there. Rememeber the following,
Rate of 
Rate of 
Pipe  = =3.333hrs=200 minutes it takes to fill the tank
Pipe  = =5 hours= 300 minutes it takes to fill the tank
.
It took 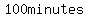 for Pipe A alone to fill the tank at first. You see above, it needs 200 minutes for A to fill 50L tank. By ratio & proportion,
x=25L (remaining volume to fill)
It just makes sense, only half of the total time he used (100 min), so only half of the tank remains (25L).
Now, to continue filling the remaining 25L, Pipe B joins the process.
We need to add the rate of Pipe A + Rate of Pipe B for the remining task:
Then,
 = 1 hour = 60 minutes
.
In conclusion, we add this 60 minutes (Both A & B) + 100 minutes (alone Pipe A)= 160 minutes
Thank you,
Jojo
|
|
|
| |
