|
Question 149802: 1. Use synthetic division to divide the polynomial 2x^3 + 7x^2 – 5 by 3+x and write the quotient and the remainder
2. Consider the polynomial f(x)= 4x^4+5x^3 + 7x^2 – 34x+8
By using the Rational Zero Theorem, list all possible rational zeros of the given polynomial.
Find all of the zeros of the given polynomial. Show procedure
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! # 1
Let's simplify this expression using synthetic division
Start with the given expression 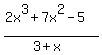
First lets find our test zero:
 Set the denominator Set the denominator  equal to zero equal to zero
 Solve for x. Solve for x.
so our test zero is -3
Now set up the synthetic division table by placing the test zero in the upper left corner and placing the coefficients of the numerator to the right of the test zero.(note: remember if a polynomial goes from  to to  there is a zero coefficient for there is a zero coefficient for  . This is simply because . This is simply because 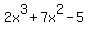 really looks like really looks like 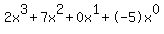
Start by bringing down the leading coefficient (it is the coefficient with the highest exponent which is 2)
Multiply -3 by 2 and place the product (which is -6) right underneath the second coefficient (which is 7)
Add -6 and 7 to get 1. Place the sum right underneath -6.
Multiply -3 by 1 and place the product (which is -3) right underneath the third coefficient (which is 0)
Add -3 and 0 to get -3. Place the sum right underneath -3.
Multiply -3 by -3 and place the product (which is 9) right underneath the fourth coefficient (which is -5)
Add 9 and -5 to get 4. Place the sum right underneath 9.
Since the last column adds to 4, we have a remainder of 4. This means  is not a factor of is not a factor of 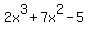
Now lets look at the bottom row of coefficients:
The first 3 coefficients (2,1,-3) form the quotient

and the last coefficient 4, is the remainder, which is placed over  like this like this
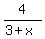
Putting this altogether, we get:
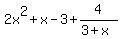
So 
which looks like this in remainder form:
 remainder 4 remainder 4
-----------------------------------
Answer:
So the quotient is  and the remainder is 4 and the remainder is 4
# 2
a)
Any rational zero can be found through this equation
 where p and q are the factors of the last and first coefficients where p and q are the factors of the last and first coefficients
So let's list the factors of 8 (the last coefficient):

Now let's list the factors of 4 (the first coefficient):

Now let's divide each factor of the last coefficient by each factor of the first coefficient

Now simplify
These are all the distinct rational zeros of the function that could occur

b)
Now let's use synthetic division to test each possible zero:
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| 1/2 | | | 4 | 5 | 7 | -34 | 8 | | | | | 2 | 7/2 | 21/4 | -115/8 | | | 4 | 7 | 21/2 | -115/4 | -51/8 |
Since the remainder 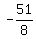 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| 1/4 | | | 4 | 5 | 7 | -34 | 8 | | | | | 1 | 3/2 | 17/8 | -255/32 | | | 4 | 6 | 17/2 | -255/8 | 1/32 |
Since the remainder  (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| 2 | | | 4 | 5 | 7 | -34 | 8 | | | | | 8 | 26 | 66 | 64 | | | 4 | 13 | 33 | 32 | 72 |
Since the remainder  (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| 4 | | | 4 | 5 | 7 | -34 | 8 | | | | | 16 | 84 | 364 | 1320 | | | 4 | 21 | 91 | 330 | 1328 |
Since the remainder 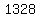 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| 8 | | | 4 | 5 | 7 | -34 | 8 | | | | | 32 | 296 | 2424 | 19120 | | | 4 | 37 | 303 | 2390 | 19128 |
Since the remainder 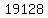 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -1 | | | 4 | 5 | 7 | -34 | 8 | | | | | -4 | -1 | -6 | 40 | | | 4 | 1 | 6 | -40 | 48 |
Since the remainder  (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -1/2 | | | 4 | 5 | 7 | -34 | 8 | | | | | -2 | -3/2 | -11/4 | 147/8 | | | 4 | 3 | 11/2 | -147/4 | 211/8 |
Since the remainder 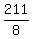 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -1/4 | | | 4 | 5 | 7 | -34 | 8 | | | | | -1 | -1 | -3/2 | 71/8 | | | 4 | 4 | 6 | -71/2 | 135/8 |
Since the remainder 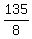 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -2 | | | 4 | 5 | 7 | -34 | 8 | | | | | -8 | 6 | -26 | 120 | | | 4 | -3 | 13 | -60 | 128 |
Since the remainder  (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -4 | | | 4 | 5 | 7 | -34 | 8 | | | | | -16 | 44 | -204 | 952 | | | 4 | -11 | 51 | -238 | 960 |
Since the remainder 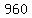 (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
------------------------------------------------------
Let's make the synthetic division table for the function  given the possible zero given the possible zero  : :
| -8 | | | 4 | 5 | 7 | -34 | 8 | | | | | -32 | 216 | -1784 | 14544 | | | 4 | -27 | 223 | -1818 | 14552 |
Since the remainder  (the right most entry in the last row) is not equal to zero, this means that (the right most entry in the last row) is not equal to zero, this means that  is not a zero of is not a zero of 
====================================
Since none of the possible rational roots are actual roots, this means that the polynomial either has irrational roots or complex roots.
|
|
|
| |