SOLUTION: In triangle ABC A=35 degrees, a=43 and c=20. Determine whether triangle ABC has no solution, one solution, or two solutions. Then solve the triangle. Round to the nearest tenth.

Algebra ->  Trigonometry-basics -> SOLUTION: In triangle ABC A=35 degrees, a=43 and c=20. Determine whether triangle ABC has no solution, one solution, or two solutions. Then solve the triangle. Round to the nearest tenth.      Log On


   

Question 149726: In triangle ABC A=35 degrees, a=43 and c=20. Determine whether triangle ABC has no solution, one solution, or two solutions. Then solve the triangle. Round to the nearest tenth.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
In triangle ABC A=35 degrees, a=43 and c=20. Determine whether triangle ABC has no solution, one solution, or two solutions. Then solve the triangle. Round to the nearest tenth.






In solving the ambiguous case, "Angle-Side-Side", "ASS", 
we use the law of sines in this fashion:



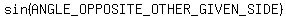Solve for sin%28ANGLE_OPPOSITE_OTHER_GIVEN_SIDE%29

1. If this is greater than 1 there are no solutions.
2. If this is less than 1, we have either one or two solutions 
3. In the rare case this equals exactly 1, the
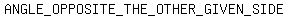   ANGLE_OPPOSITE_THE_OTHER_GIVEN_SIDE is 90°, and you 
   solve it as a right triangle.

In case 2, 

I. use the inverse sine button on your calculator to find one 
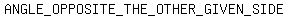certain possibility for the ANGLE_OPPOSITE_THE_OTHER_GIVEN_SIDE.

II. Find the supplement of the angle found in step I, by subtracting
    from 180°.

III. Add the result of step II to the given angle and subtract from
     180°.

IV.  If the result of III is negative there is only one solution. If it
     is positive then there are two solutions, one with the result of II
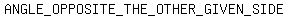     and one with the result of III for the ANGLE_OPPOSITE_THE_OTHER_GIVEN_SIDE.


In your problem we use the law of sines in this fashion:

%28GIVEN_OPPOSITE_SIDE_OF_GIVEN_ANGLE%29=a=43

%28GIVEN_ANGLE%29=35°

%28OTHER_GIVEN_SIDE%29=c=20

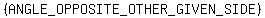%28ANGLE_OPPOSITE_OTHER_GIVEN_SIDE%29 is the unknown angle C

a%2Fsin%28A%29%2Fsin%28C%29=c%2Fsin%28C%29

43%2Fsin%2835%29%2Fsin%28C%29=20%2Fsin%28C%29

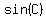
Solve for sin%28C%29

sin%28C%29+=+20sin%2835%29%2F43+=+0.2667797378

This is less than 1, so we have case 2 above, and
there is either one or two solutions. So

I. We use the inverse sine button on the calculator to find one 
certain solution for the angle C.

angle C = 15.47273197°

II. Find the supplement of that angle, by subtracting from 180°:

180° - 15.47273197° = 164.527268°

III. Add the result of step II to the given angle and subtract from
     180°.

164.527268° + 35° = 199.527268°

180° - 199.527268° = -19.52726803°.

 
IV.  This result is negative, so there is only one solution. 

Now to find the other parts.  We can find angle B by adding
the given angle A = 35° to Angle C = 15.47273197°, and then
subtracting from 180° to find Angle B:

35° + 15.47273197° = 50.47273197°

180° - 50.47273197° = 129.527268° = Angle B

Using the law of sines again to find side b

b%2Fsin%28B%29=a%2Fsin%28A%29

b=%28a%2Asin%28B%29%29%2Fsin%28A%29+=+%2843sin%28129.527268%29%29%2Fsin%2835%29=57.82461456

So we round everything to the nearest tenth:

angle C = 15.5°, angle B = 129.5°, side b = 57.8

Edwin