Question 149493: In a shop there are 20 customers, 18 of whom will make a purchase. If three customers are selected, one at a time, at random, what is the probability that all will make a purchase? Is it 0.7717, 0.7605, 0.8524, or 0.8808.
Please help
Found 2 solutions by Edwin McCravy, stanbon:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a shop there are 20 customers, 18 of whom will make a purchase. If three customers are selected, one at a time, at random, what is the probability that all will make a purchase? Is it 0.7717, 0.7605, 0.8524, or 0.8808.
Please help
It's not any of those. It's 0.7158
P(1st chosen will purchase
AND
2nd chosen will purchase
AND
3rd chosen will purchase)
=
P(1st chosen will purchase)
TIMES
P(2nd chosen will purchase, given that the 1st chosen will purchase)
TIMES
P(3rd chosen will purchase, given that the 1st and 2nd chosen will purchase)
=
 or rounded to ten-thousandths, or rounded to ten-thousandths,
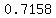 .
You can also do it using combinations: .
You can also do it using combinations:
 =
=
 Stanbon's solution is incorrect because
the choices are not independent. Binomial
probabilities are ONLY for independent choices.
The choices are not independent because the
probability of selecting the second one as a
purchaser CHANGES after selecting the first one.
Also the probability of selecting the third one
as a purchaser CHANGES after selecting the
first two.
Edwin
Stanbon's solution is incorrect because
the choices are not independent. Binomial
probabilities are ONLY for independent choices.
The choices are not independent because the
probability of selecting the second one as a
purchaser CHANGES after selecting the first one.
Also the probability of selecting the third one
as a purchaser CHANGES after selecting the
first two.
Edwin
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a shop there are 20 customers, 18 of whom will make a purchase.
-----------
P(a random person in the group makes a purchase) = 18/20 = 9/10
-----------------
If three customers are selected, one at a time, at random, what is the probability that all will make a purchase?
-----------------
This is a binomial problem with p=0.9
P(3 of 3 make a purchase) = 0.9^3 = 0.729
------------
Cheers,
Stan H.
Is it 0.7717, 0.7605, 0.8524, or 0.8808.
|
|
|