Question 149086: Write an equation of the Line 1 passing through (3,-4) that is parallel to the Line II 5x-3y-9=0. Does the line I pass through the point (6,7)? Does the line II pass through the point (6,7)?
Answer by Electrified_Levi(103)   (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Write an equation of the Line 1 passing through (3,-4) that is parallel to the Line II 5x-3y-9=0. Does the line I pass through the point (6,7)? Does the line II pass through the point (6,7)?
.
First, we have to put Line II in slope-intercept form (y = Ax+b)("A" is the slope)
.
5x-3y-9=0
.
We will move (-3y) to the right side
.
5x - 3y + 3y - 9 = 0 + 3y
.
5x - 9 = 3y
.
3y = 5x - 9
.
We will now divide each side by "3"
.
.
y =  x - 3
.
(y = x - 3) is the slope-intercept form of Line II
.
Since Line I is parallel to Line II, it has the same slope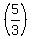 
.
Equation to Line I
.
y = x + b
.
We can solve "b" by replacing "x" and "y" with (3,-4)(x,y)(Since the line contains that point
.
.
We will multiply the right side
.
.
We will move "5" to the left side
.
.
.
b = (-9), we can replace "b" in our equation
.
y = x + b
.
y = x + (-9)
.
y = x - 9
.
(y = x - 9) is the slope-intercept equation to Line I
.
You can check by replacing "x" and "y" with (3, -4)(x,y)
.
.
.
.
(y = x - 9) is the correct equation to Line I
.
y = x - 9( to get a different form of equation, you get rid of the fraction)(We will multiply each side by "3")
.
.
3y = 5x - 27
.
We will move "3y" to the right side
.
3y - 3y = 5x - 3y - 27
0 = 5x - 3y - 27
(5x - 3y - 27 = 0) is another form,( you can move (-27) over, and it will become  ( this is the standard form)
.
To see if (6,7) is a point of either of the two lines, you will replace "x" and "y" with (6,7)(x,y)
.
First equation,
.
.
.
.
 This is not true, so point (6,7) is not a point on the first line.
.
Second line
.
5x-3y-9=0 ( standard form = (5x - 3y = 9)(moved (-9) to the right side)
.
5x - 3y = 9
.
We can replace "x" and "y" with (6,7)(x,y)
.
5(6) - 3(7) = 9
.
30 - 21 = 9
.
(9 = 9) This is true, (6,7) is a point on Line II
.
Hope I helped, Levi
|
|
|
