Question 148655: 1. A trapezoid has two 65-degree angles and 9-inch and 12-inch parallel sides. How long are the non-parallel sides? What is the area enclosed by this figure?
Answer by jojo14344(1513)   (Show Source):
You can put this solution on YOUR website! Let's name the parallel sides as  and 
And the non parallel sides as "c=?" and "d=?".
Before I proceed farther, I suggest you draw it on your own while we discuss it by words so you can follow better (just a suggestion).
.
Now from that starting point and also the endpoint of that 9 inches which is  , draw a line all the way down to  which is perpendicular right? --> mark these lines as "h" (for height),likewise the 2 lines are parallel, and that line inside these parallel lines on also measures 9 inches right (of course) ---> mark it 
.
Now you have remaining length of 3 inches,
And these 3 inches will be cut into half, 1-1/2" on one side, likewise 1-1/2" on the other. Why? Because you have opposite similar 65 deg angle right? (If not the same angle, the length won't be the same)
The 1-1/2" length mark one side as  and the other as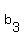 
.
Can you follow still?
Now, side "c", "h" and forms a right triangle (if you mark them properly) with angle 65 deg. To get "c",
 = 1.5/cos65
c=3.55 inches = d -------------> length of the non parallel sides
.
For area in the trapezoid,
A=1/2(h)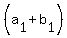
To get "h", 
h=(sin65)(3.55)=3.22 inches
Therefore,
A=(1/2)(3.22){9+12}
A=33.81 sq inches
Thank you,
Jojo
|
|
|
