Prove the identity:

Replace 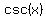 on left side by
on left side by 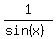 Replace
Replace  on left side by
on left side by 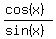
 Combine the numerators over the common denominator:
Combine the numerators over the common denominator:
 Form the conjugate of the numerator by changing the sign
of the second term:
Form the conjugate of the numerator by changing the sign
of the second term: 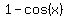 , put it over itself,
like this
, put it over itself,
like this 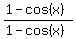 , which equals 1,
so we can multiply by it without changing the value:
, which equals 1,
so we can multiply by it without changing the value:
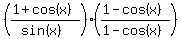 Indicate the multiplications of the tops and bottoms:
Indicate the multiplications of the tops and bottoms:
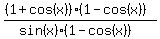 FOIL out the top:
FOIL out the top:
 Simplify by canceling in the top:
Simplify by canceling in the top:
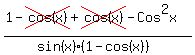
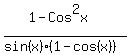 Replace
Replace 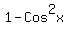 by
by 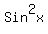
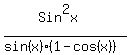 The
The  in the bottom cancels out the
square in the top:
in the bottom cancels out the
square in the top:
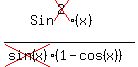
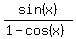 Edwin
Edwin