Question 148405: 24. From the list of plotted points
(-5,5) (3,5)
(-4, 3/2) (2, 3/2)
(-3,-1) (1,-1)
(-2, -5/2) (0, -5/2)
(-1,-3)
Form an equation after plotting these points and then answer the questions below:
Is the degree of the polynomial odd or even?
Is the leading coefficient of the polynomial positive or negative?
Number of zeros
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! If we plot the points we get

Now draw a curve through these points to get the equation:

From the graph, we can see that the degree is even (since both ends of the graph go in the same y direction). Also, we can see that the leading coefficient is positive (since the graph opens upward). Finally, we can see that there are two zeros (since there are two x-intercepts).
------------------------------------------------------
Since we have all of this info, we don't need the equation. However, if you do need the equation, this is how you would find it:
From the graph, we can see that the vertex is (-1,-3).
 Start with the general vertex equation. Start with the general vertex equation.
 Plug in Plug in  and and 
 Simplify. Simplify.
Now let's plug in another point. Let's plug in (1,-1)
 Plug in Plug in  and and 
 Add Add
 Square 2 to get 4. Square 2 to get 4.
 Add Add  to both sides. to both sides.
 Subtract Subtract 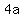 from both sides. from both sides.
 Combine like terms on the right side. Combine like terms on the right side.
 Divide both sides by Divide both sides by  to isolate to isolate  . .
 Reduce. Reduce.
So this means that the equation is 
 FOIL FOIL
 Distribute Distribute
 Multiply Multiply
 Combine like terms. Combine like terms.
So the equation that goes through the points is 
From the equation, we can see that the degree of the polynomial is even. Also, we can see that the leading coefficient is positive since  . Finally, if we use the quadratic formula, we'll find that the polynomial . Finally, if we use the quadratic formula, we'll find that the polynomial  has 2 zeros. has 2 zeros.
|
|
|