Question 148339: Solve the System:
2x-y+2z=11
3x-2y-z=12
x-3y-z=1
Answer by Electrified_Levi(103)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help
.
Solve the System:
2x-y+2z=11
3x-2y-z=12
x-3y-z=1
.
There are several different ways you can solve these kind of problems.( There really isn't any fast simple way to solve these equations) (There is substitution, elimination, and others)
.
The way I usually solve 2 system, or 3 system equations(we will just give it a name)(our's is a 3 system, it has three variables) I think it is a pretty easy way to solve equations(you can solve any 2 system, 3 system, and even 4 system equations with this method)
.
First you need to solve for a letter.( we will use the first two equations first, then we will need to do the last two(we can use the middle equation twice)) You will usually want to solve for the easiest letter, in this case "z"
.
We will need to solve "z" in all our equations, we will do the first, second, then third.
.
First equation
.
2x-y+2z=11
.
We will move the "2x" and (-y) to the right side("z" is already positive)
.
2x -2x - y + y +2z = 11 - 2x + y
2z = 11 - 2x + y
2z = -2x + y + 11
.
We will divide everything by "2"
.

.
In our first equation 
.
We will now solve "z" in our second equation
.
3x-2y-z=12
.
We will move the (-z) to the right side
.
3x - 2y - z + z = 12 + z
3x - 2y = 12 + z
3x - 2y = z + 12
.
We will move "12" to the left side
.
3x - 2y - 12 = z + 12 - 12
3x - 2y - 12 = z
.
In our second equation, z = ( 3x - 2y - 12)
.
Now we will do our third equation now
.
x-3y-z=1
.
We will move (-z) to the right side
.
x - 3y - z + z = 1 + z
x - 3y = 1 + z
x - 3y = z + 1
.
We will move "1" to the left side
.
x -3y - 1 = z + 1 - 1
x -3y - 1 = z
.
In our third equation, z = ( x - 3y - 1)
.
Since "z" is equal to one number, all of our answer will equal each other
.

.
We will now solve even more, we will use the first two answers, then the last two( middle answer is used twice)
.

.

.
We will use cross multiplication
.
-2x + y + 11 = 2( 3x - 2y - 12)
-2x + y + 11 = 6x - 4y - 24
.
We will make the "x" positive, and "y" negative( we will move (-2x) and "y" to the right side)
.
-2x + 2x + y - y + 11 = 6x + 2x - 4y - y - 24
11 = 8x - 5y - 24
.
We will move "-24" to the left side
.
11+24 = 8x - 5y - 24 + 24
35 = 8x - 5y
.
Our first answer is (8x - 5y = 35) (It is a 2 system equation)
.
Now we will solve using the last two equations
.
( 3x - 2y - 12) = (x - 3y - 1)
3x - 2y - 12 = x - 3y - 1
.
We will move "x" and (-3y) to the left side
.
3x - x - 2y + 3y - 12 = x - x - 3y + 3y - 1
2x + y - 12 = -1
.
We will move (-12) to the right side
.
2x + y - 12 + 12= -1 + 12
2x + y = 11
.
Our second answer is equal to (2x + y = 11)
.
We will need to put the two answers we got together(not add them, but put them side by side)
.
(8x - 5y = 35)
(2x + y = 11)
.
We will need to solve for a letter again, the easiest is "y"
.
First equation
.
(8x - 5y = 35)
.
We will need to move (-5y) to the right side
.
8x - 5y + 5y = 35 + 5y
.
8x = 35 + 5y
.
8x = 5y + 35
.
We will move 35 to the left side
.
8x - 35 = 5y + 35 - 35
8x - 35 = 5y
.
We will divide everything by "5"
.

.

.

.
Our first answer is 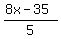
.
Now we will solve "y" using the second equation
.
(2x + y = 11)
.
We will move "2x" to the right side
.
2x - 2x + y = 11 - 2x
y = (11 - 2x)
y = -2x + 11
.
Our second answer is (-2x + 11)
.
We will put our two answers in equation form, since they equal each other
.

.

.
We will use cross multiplication
.
8x - 35 = 5( -2x + 11)
8x - 35 = -10x + 55
.
We will move the (-10x) to the left
.
8x + 10x - 35 = -10x + 10x + 55
18x - 35 = 55
.
We will move (-35) to the right side
.
18x - 35 + 35 = 55 + 35
18x = 90
.
We will divide everything by 18
.

.
x = 5
.
We found "x", which is "5".
.
To find "y" we can replace "x" with 5, in one of our 2 system equations( we will use the easier one)
.
2x + y = 11
.
2(5) + y = 11
10 + y = 11
.
We will move 10 to the right side
.
10 - 10 + y = 11 - 10
y = 1
.
x = 5
y = 1
.
We can check by replacing "x" and "y" in the other 2 system equation
.
8x - 5y = 35
.
8(5)-5(1) = 35
40 - 5 = 35
35 = 35
.
We know that ( x = 5) and (y = 1), we can replace "x" and "y" in one of our original 3 system equations, to solve for "z"
.
2x-y+2z=11
3x-2y-z=12
x-3y-z=1
.
We will use the third equation(it is the easiest)
.
x-3y-z=1
.
(5)-3(1)-z=1
5 - 3 - z=1
2 - z = 1
.
We will move (-z) to the right side
.
2 - z + z = 1 + z
2 = 1 + z
2 = z + 1
.
We will move "1" to the left side
.
2 - 1 = z + 1 - 1
1 = z
z = 1
.
x = 5
y = 1
z = 1
.
We can check by replacing "x", "y" , and "z" in any of the 3 system equations
.
2x-y+2z=11
3x-2y-z=12
x-3y-z=1
.
2x-y+2z=11
.
2(5)-(1)+2(1)=11
10 - 1 + 2 = 11
11 = 11
.
3x-2y-z=12
.
3(5)-2(1)-(1)=12
15 - 2 - 1 = 12
12 = 12
.
x-3y-z=1
.
(5) - 3(1) - (1) = 1
5 - 3 - 1 = 1
1 = 1
.
The answers to the 3 system equations are:
.
x = 5
y = 1
z = 1
.
The solution set is written as (x,y,z)
.
Our solution set = (5,1,1)
.
Hope I helped, Levi
|
|
|