|
Question 148258: John increased the area of his garden by 120 ft^2. The original garden was 12 ft. by 14 ft., and he increased the length and the width by the same amount. Find the exact dimensions of the new garden and approximate the dimensions in feet and inches.
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x=amount he increased the dimensions of his garden, 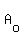 =area of original garden and =area of original garden and  =area of new garden =area of new garden
Since the original garden is 12 ft by 14 ft, this means that the area of the original garden is

So  which means that the area of the original garden is 168 ft^2 which means that the area of the original garden is 168 ft^2
Because the area of the new garden is 120 ft^2 larger than the original garden, this means that 
 Plug in Plug in 
 Add Add
So the area of the new garden is 288 ft^2
Now since he increased the dimensions by some unknown amount, this means that the area of the new garden is equal to:

 Plug in Plug in 
 FOIL FOIL
 Subtract 288 from both sides. Subtract 288 from both sides.
 Combine and rearrange the terms. Combine and rearrange the terms.
Let's use the quadratic formula to solve for x
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Square Square 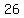 to get to get  . .
 Multiply Multiply 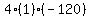 to get to get 
 Rewrite Rewrite 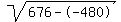 as as 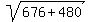
 Add Add  to to 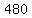 to get to get 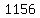
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 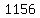 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible answers are  or or 
However, since a negative length is not possible, this means that he increased his garden by 4 feet.
Now simply add 4 to each dimension 12 and 14 to get:
12+4=16 by 14+4=18
So the dimensions of the new garden are
16 ft by 18 ft
note: the approximate answers are the same as the exact answers since there are no square roots, fractions, decimals, etc. in the answer
|
|
|
| |