SOLUTION: 2. Out for a walk in Chicago, Morgan measured the angle of elevation to the distant Sears Tower, and got 3.6 degrees. After walking one km directly toward the building, Morgan foun

Algebra ->  Trigonometry-basics -> SOLUTION: 2. Out for a walk in Chicago, Morgan measured the angle of elevation to the distant Sears Tower, and got 3.6 degrees. After walking one km directly toward the building, Morgan foun      Log On


   

Question 148154: 2. Out for a walk in Chicago, Morgan measured the angle of elevation to the distant Sears Tower, and got 3.6 degrees. After walking one km directly toward the building, Morgan found that the angle of elevation had increased to 4.2 degrees. Use this information to estimate the height of the Sears Tower and how far Morgan is from it after walking toward the building.
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
First draw the picture and label the angles and sides:


Photobucket - Video and Image Hosting




Now let's find the measures of the other angles. From the drawing, we can see that the angle 4.2 degrees and the unkown angle "a" make up a straight line. So this means that a%2B4.2=180. Solving for "a", we get a=175.8.


Using the fact that all angles in a triangle add to 180 degrees, this means that 175.8%2B3.6%2Bb=180 (these are the angles from the obtuse triangle). Solving for "b" gives us b=0.6.

Finally, we know that angles "c" and 4.2 are complementary. So this means that c%2B4.2=90. Isolate "c" and we get c=85.8


Now add these angle measures to the drawing.


Photobucket - Video and Image Hosting





Notice how we have a lot of angle measures but only one side length given. We can use the Law of Sines to find any given length of any triangle as long as we have at least two angles and a side length.

So the Law of Sines formula is:
sin%28A%29%2Fa=sin%28B%29%2Fb=sin%28C%29%2Fc

Since we have two angles and a side, let's use the angle measures 3.6 and 0.6 to find the length of "y"

sin%28A%29%2Fa=sin%28B%29%2Fb


sin%283.6%29%2Fy=sin%280.6%29%2F1 Plug in A=3.6, a=y, B=0.6, and b=1


sin%283.6%29%2Fy=sin%280.6%29 Simplify.


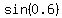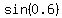sin%283.6%29=y%2Asin%280.6%29 Multiply both sides by sin%280.6%29.


sin%283.6%29%2Fsin%280.6%29=y Divide both sides by sin%280.6%29.


y=sin%283.6%29%2Fsin%280.6%29 Rearrange the equation.


y=%280.06279%29%2F%280.01047%29 Evaluate the sine functions.


y=5.99616 Divide.


So the length of "y" is 5.99616 km


Now let's update the drawing


Photobucket - Video and Image Hosting





From the drawing, we can see that the hypotenuse of the second triangle is 5.99616. Using the angle 4.2, this makes the height of the building "x" the opposite side. So let's use the sine function


sin%28a%29=opposite%2Fhypotenuse where "a" is the angle 4.2


sin%284.2%29=x%2F5.99616 Plug in a=4.2 and the given side lengths


5.9961%2Asin%284.2%29=x Multiply both sides by 5.99616.


5.9961%280.07324%29=x Evaluate the sine of 4.2.


0.43915=x Multiply


So the height is x=0.43915. Now to find the length of the base of the second triangle, simply use the cosine function.



cos%28a%29=adjacent%2Fhypotenuse where "a" is the angle 4.2


cos%284.2%29=x%2F5.99616 Plug in a=4.2 and the given side lengths


5.9961%2Acos%284.2%29=x Multiply both sides by 5.99616.


5.9961%280.99731%29=x Evaluate the cosine of 4.2.


5.97997=x Multiply



So the distance from the building to the second position is 5.97997 km


---------------------------------
Answer:

So the height of the building is 0.43915 km or 1,440.78084 feet and the distance from the building to Morgan's final position is 5.97997 km or 19,619.3241 feet