Question 148112: The Product of two consecutive positive intergers is 1 more than their sum. Find the intergers.
Found 2 solutions by checkley77, Electrified_Levi:
Answer by checkley77(12844)   (Show Source):
You can put this solution on YOUR website! x(x+1)=x+x+1+1
x^1+x=2x+2
x^2+x-2x-2=0
x^2-x-2=0
(x-2)(x+1)=0
x-2=0
x=2 for the smaller integer.
2+1=3 for the larger integer
proof:
2*3=2+3+1
6=6
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
The Product of two consecutive positive integers is 1 more than their sum. Find the integers.
.
The first integer is "x", the second is (x+1)
.
consecutive means one after the other, if there was a third, fourth, and fifth integer it would be (x+2),(x+3),(x+4)(You will do this on any problem where it says consecutive(unless it says consecutive odd, or even, then you add "2" each time
.
Now we can do the equation
.
The Product of two consecutive positive integers is 1 more than their sum.
.
(x)(x+1) = (x)+(x+1)+1
.
We will use the distributive property
.
.
.
.
We will move everything on the left side
.
.
.
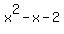 has factors of (x+1), and (x-2) ( factors of (-2) add up to (-1))
.
We can now solve for "x", using one factor at a time.
.
First factor
(x+1)=0
x+1=0
x+1-1=0-1
.
x=(-1)
.
Second factor
(x-2)=0
x-2=0
x-2+2=0+2
.
x = 2
.
You can check by replacing "x" with (-1), or 2, in the equation
.
( We will only check one answer, (2)
.
.
.
.
The first integer is x, or 2(It asked for a positive integer), the second integer is (x+1), or 3
.
You can check by replacing "x" with 2 in
.
(x)(x+1) = (x)+(x+1)+1
.
(2)(2+1) = (2)+(2+1)+1
.
(2)(3) = (2)+(3)+1
.
6 = 6
.
First integer = 2
Second integer = 3
.
Hope I helped, Levi
|
|
|
