SOLUTION: Find the vertex and intercepts for this parabola: g(x) = x^2 + x - 6 This is how I have worked it: a = 1, b = 1, c = -6 x = -b/2a x = -1/[2(1)] = -1/2 g(-1/2) = (-1/2

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the vertex and intercepts for this parabola: g(x) = x^2 + x - 6 This is how I have worked it: a = 1, b = 1, c = -6 x = -b/2a x = -1/[2(1)] = -1/2 g(-1/2) = (-1/2      Log On


   

Question 148000: Find the vertex and intercepts for this parabola:
g(x) = x^2 + x - 6
This is how I have worked it:
a = 1, b = 1, c = -6
x = -b/2a
x = -1/[2(1)] = -1/2
g(-1/2) = (-1/2)^2 + (-1/2) - 6
= 25/2
So, the vertex is (-1/2, 25/2)
Am I correct so far?
How do I verify that I am correct? What should my next step be?
I appreciate your help very much! Thank you!
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Vertex:



In order to find the vertex, we first need to find the x-coordinate of the vertex.


To find the x-coordinate of the vertex, use this formula: x=%28-b%29%2F%282a%29.


x=%28-b%29%2F%282a%29 Start with the given formula.


From y=x%5E2%2Bx-6, we can see that a=1, b=1, and c=-6.


x=%28-%281%29%29%2F%282%281%29%29 Plug in a=1 and b=1.


x=%28-1%29%2F%282%29 Multiply 2 and 1 to get 2.


So the x-coordinate of the vertex is x=-1%2F2. Note: this means that the axis of symmetry is also x=-1%2F2.


Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.


y=x%5E2%2Bx-6 Start with the given equation.


y=%28-1%2F2%29%5E2-1%2F2-6 Plug in x=-1%2F2.


y=%28-1%2F2%29%5E2-1%2F2-6 Plug in x=-1%2F2.


y=1%2F4-1%2F2-6 Square -1%2F2 to get 1%2F4.


y=-25%2F4 Combine like terms.


So the vertex is


note: you can verify this with a calculator. You can use the "min/max" feature.

------------------------------------------------------------------

Intercepts:



x-intercept:


To find the x-intercept, plug in y=0 and solve for x


y=x%5E2%2Bx-6 Start with the given equation.


0=x%5E2%2Bx-6 Plug in y=0


%28x%2B3%29%28x-2%29=0 Factor the left side (note: if you need help with factoring, check out this solver)



Now set each factor equal to zero:
x%2B3=0 or x-2=0

x=-3 or x=2 Now solve for x in each case

So the x-intercepts are (-3,0) and (2,0)


-------------

y-intercept:


To find the y-intercept, plug in x=0 and simplify

y=x%5E2%2Bx-6 Start with the given equation.


y=0%5E2%2B0-6 Plug in x=0


y=-6 Simplify

So the y-intercept is (0,-6)


-----------------------------


Notice if we graph y=x%5E2%2Bx-6 we can visually verify our answers.


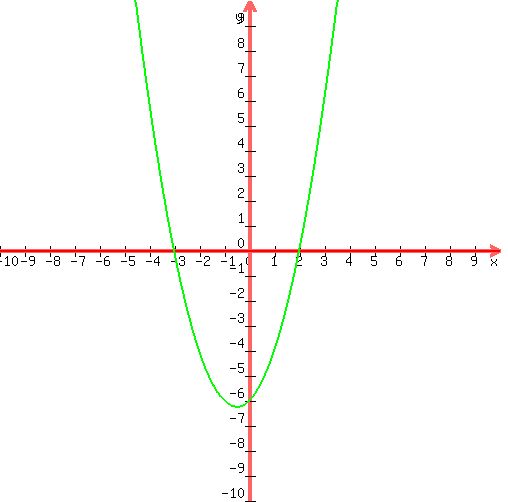+graph%28500%2C500%2C-10%2C10%2C-10%2C10%2C0%2C+x%5E2%2Bx-6%29+ Graph of y=x%5E2%2Bx-6