Question 147722: Please solve, show work and include all relevant points (i.e vertices, intercepts, foci,directrix,asymptotes, ect..)
x^2-4y^2+2x=32y=67
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Complete the square in both x and y.





This is an equation for a hyperbola which has a general form of



Center of the hyperbola is (h,k) or in this case (-1,-4)
Distance between the foci is 2c where



The eccentricity,e, is then

The foci of the hyperbola are located at
(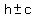 , , )=( )=(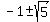 , , ) )
The vertices of the hyperbola are located at
(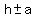 , , )=( )=(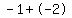 , , )=(-3,-4) and (1,-4) )=(-3,-4) and (1,-4)
The equation of the asymptote lines is given by


The directrix of a hyperbola is given by



|
|
|