SOLUTION: One angle of a triangle is 3 times as large as another. The third angle is twice the sum of the first 2 angles. What is the measure of the largest angle?

Algebra ->  Angles -> SOLUTION: One angle of a triangle is 3 times as large as another. The third angle is twice the sum of the first 2 angles. What is the measure of the largest angle?       Log On


   

Question 147584: One angle of a triangle is 3 times as large as another. The third angle is twice the sum of the first 2 angles. What is the measure of the largest angle?
Answer by mangopeeler07(462) About Me  (Show Source):
You can put this solution on YOUR website!
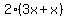First, set a variable for the smallest angle. How about x? So according to the question, the values for the angles in terms of x would be x, 3x, and 2(3x+x). The angles of a triangle add up to 180 degrees, so set up an equation like thisx%2B3x%2B2%283x%2Bx%29=180 Then distribute the two and get x%2B3x%2B6x%2B2x=180. Then combine like terms and get 12x=180 and then divide both sides by 12 and get x=180%2F12 which reduces to 15. That is the smallest angle. To get the largest angle, plug in 15 for x in the original value that you assigned to that angle (2%283x%2Bx%29). 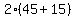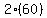You should get 2%2845%2B15%29 or 2%2860%29. That is 120. So the biggest angle is 120.

To check, plug in 15 for all the x's in the original equation 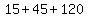x%2B3x%2B2%283x%2Bx%29=180. You should get 15%2B45%2B120, or 120+60, which is 180, so it all works out.

The angle measures are 120, 45, and 15.