SOLUTION: It asks, without drawing the graph of the given equation, determine: How many x-intercepts the parabola has,wether its vertex lies above or below or on the x-axis. The problem is

Algebra ->  Coordinate-system -> SOLUTION: It asks, without drawing the graph of the given equation, determine: How many x-intercepts the parabola has,wether its vertex lies above or below or on the x-axis. The problem is       Log On


   

Question 147536This question is from textbook algebra
: It asks, without drawing the graph of the given equation, determine: How many x-intercepts the parabola has,wether its vertex lies above or below or on the x-axis.
The problem is y=-x^2+2x-1. I have a hard time understanding how to solve it, please help me. Thank you=) This question is from textbook algebra

Found 2 solutions by jim_thompson5910, mangopeeler07:
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
How many x-intercepts does the parabola have?

To find this out, we need to find out how many solutions there are. So we need to use the discriminant formula D=b%5E2-4ac.


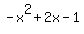From -x%5E2%2B2x-1 we can see that a=-1, b=2, and c=-1


D=b%5E2-4ac Start with the discriminant formula


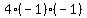D=%282%29%5E2-4%28-1%29%28-1%29 Plug in a=-1, b=2, and c=-1


D=4-4%28-1%29%28-1%29 Square 2 to get 4


D=4-4 Multiply 4%28-1%29%28-1%29 to get %28-4%29%28-1%29=4


D=0 Subtract 4 from 4 to get 0


Since the discriminant is equal to zero, this means that there is only one real solution.

Since there is only one real solution, there is only one x-intercept. Because there is only one x-intercept, this means that the vertex must lie on the x-axis. However, this may not be so obvious. So let's find out where the vertex is.



--------------------------------------------------------


Where does the vertex lie?

To find out if the vertex is above or below the x-axis, we need to find the y-coordinate of the vertex. However, we first need to find the x-coordinate of the vertex.

To find the x-coordinate of the vertex, use this formula: x=%28-b%29%2F%282a%29.


x=%28-b%29%2F%282a%29 Start with the given formula.


From 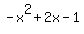-x%5E2%2B2x-1, we can see that a=-1, b=2, and c=-1.


x=%28-%282%29%29%2F%282%28-1%29%29 Plug in a=-1 and b=2.


x=%28-2%29%2F%28-2%29 Multiply 2 and -1 to get -2.


x=1 Divide.


So the x-coordinate of the vertex is x=1. Note: this means that the axis of symmetry is also x=1.


Now that we know the x-coordinate of the vertex, we can use it to find the y-coordinate of the vertex.


y=-x%5E2%2B2x-1 Start with the given equation.


y=-%281%29%5E2%2B2%281%29-1 Plug in x=1.


y=-1%2B2%281%29-1 Square 1 to get 1.


y=-1%2B2-1 Multiply 2 and 1 to get 2.


y=0 Combine like terms.


So the y-coordinate of the vertex is y=0, which means that the the vertex is on the x-axis. So this confirms our original claim.


Answer by mangopeeler07(462) About Me  (Show Source):
You can put this solution on YOUR website!
Here's an easy solution, step by step, no formulas involved: the x-intercept is whatever x is when y is zero. factor the original equation by taking out negative one and then factoring 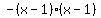-%28x-1%29%28x-1%29. Set it equal to zero. Then solve for each expression individually to equal zero. What minus 1 equals zero? You should have gotten 1 for both. That means the x-intercept is 1. There is only one x-intercept because you got the same solution for x in both expressions. Since there is only 1, it lies on the x-axis.

**Just in case you're wondering whether the parabola opens up or down, it opens down. Whenever x%5E2 is positive, it moves up, and vice versa. Think of it this way: If your x%5E2 is positive, then y wants to be positive too, so it moves upward. If your x%5E2 is negative, then y wants to be negative too, so it moves downward.**