SOLUTION: I need help, if you may. It says without drawing the graph of the given equation, determine: How many x-intercepts the parabola had and whether its vertex lies above or below or on

Algebra ->  Graphs -> SOLUTION: I need help, if you may. It says without drawing the graph of the given equation, determine: How many x-intercepts the parabola had and whether its vertex lies above or below or on      Log On


   

Question 147230This question is from textbook algebra
: I need help, if you may. It says without drawing the graph of the given equation, determine: How many x-intercepts the parabola had and whether its vertex lies above or below or on the x-axis.
y=x^2-5x+6
Thank you=) This question is from textbook algebra

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
To figure out how many x-intercepts there are, we need to find out how many solutions there are. So let's use the discriminant formula D=b%5E2-4ac.

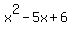From x%5E2-5x%2B6 we can see that a=1, b=-5, and c=6


D=b%5E2-4ac Start with the discriminant formula


D=%28-5%29%5E2-4%281%29%286%29 Plug in a=1, b=-5, and c=6


D=25-4%281%29%286%29 Square -5 to get 25


D=25-24 Multiply 4%281%29%286%29 to get %284%29%286%29=24


D=1 Subtract 24 from 25 to get 1


Since the discriminant is greater than zero, this means that there are two real solutions. So there are two distinct x-intercepts.

As a quick note, since there are two distinct x-intercepts, this means that the vertex cannot be on the x-axis. So it is either above or below the x-axis.
---------------------------------------------


To find out if the vertex is above or below the x-axis, we need to find the y-coordinate of the vertex. To do that, we need to find the x-coordinate of the vertex.


So let's use this formula to find the x-coordinate of the vertex.

x=-b%2F%282a%29

From the equation y=x%5E2-5x%2B6 we can see that a=1 and b=-5

x=%28--5%29%2F%282%2A1%29 Plug in b=-5 and a=1


x=5%2F%282%2A1%29 Negate -5 to get 5


x=%285%29%2F2 Multiply 2 and 1 to get 2


So the x-coordinate of the vertex is x=5%2F2. Lets plug this into the equation to find the y-coordinate of the vertex.


y=x%5E2-5x%2B6 Start with the given polynomial


y=%285%2F2%29%5E2-5%285%2F2%29%2B6 Plug in x=5%2F2


y=25%2F4-5%285%2F2%29%2B6 Square 5%2F2 to get 25%2F4


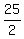
y=25%2F4-25%2F2%2B6 Multiply 5 by 5%2F2 to get 25%2F2


y=-1%2F4 Now combine like terms


So the vertex is


Since the y-coordinate of the vertex is y=-1%2F4, this means that the vertex is below the x-axis